主题
Search

二项式系数

下载 Mathematica Notebook下载 Wolfram Notebook

二项式系数 (n; k) 是从 n 个可能性中选取 k 个无序结果的方式数，也称为组合或组合数。符号 _nC_k 和 (n; k) 用于表示二项式系数，有时读作“n 选择 k”。

(n; k) 因此给出了从一组 n 个不同项目中可能存在的 k-子集 的数量。例如，{1,2,3,4} 的 2-子集是六对 {1,2}, {1,3}, {1,4}, {2,3}, {2,4}, 和 {3,4}，因此 (4; 2)=6。此外，从原点 (0,0) 到点 (a,b) 的 格路路径 的数量是二项式系数 (a+b; a) (Hilton and Pedersen 1991)。

对于 非负整数 n 和 k，且满足 0<=k<=n，二项式系数值由下式给出

(n; k)=(n!)/(k!(n-k)!)
(1)

(Graham et al. 1989, p.157)，其中 z! 表示阶乘。对于递增的 n，按行填充 k=0, 1, ..., n 的值，得到帕斯卡三角形。

将阶乘写为伽玛函数 z!=Gamma(z+1) 允许将二项式系数推广到非整数参数（包括复数 x 和 y），形式为

(x; y)=(Gamma(x+1))/(Gamma(y+1)Gamma(x-y+1)).
(2)

罗马系数 (Roman 1992, Loeb 1995) 是二项式系数的推广。每当定义二项式系数时，罗马系数都与之一致。然而，罗马系数是为二项式系数未定义的值定义的。

对于 非负整数 y 的二项式系数给出了一个关于 x 的多项式

(x; y)=((x)_y)/(y!)
(3)
=(x(x-1)(x-2)...(x-y+1))/(y(y-1)...2·1),
(4)

其中 (x)_y 是一个 泊松-丘哈默符号。这些有理系数有时被称为“广义二项式系数”。

使用伽玛函数对称公式

(Gamma(s-a+1))/(Gamma(s-b+1))=(-1)^(b-a)(Gamma(b-s))/(Gamma(a-s))
(5)

对于整数 a, b 和复数 s，此定义可以扩展到负整数参数，使其在所有整数参数处连续，以及在所有复数参数处连续，除了负整数 x 和非整数 y 的情况，在这种情况下它是无限的 (Kronenburg 2011)。这个定义，由下式给出

(n; k)={(-1)^k(-n+k-1; k) for k>=0; (-1)^(n-k)(-k-1; n-k) for k<=n; 0 otherwise
(6)

对于负整数 n 和整数 k，与二项式定理以及组合恒等式一致，但有一些特殊例外 (Kronenburg 2011)。

二项式系数在 Wolfram 语言 中实现为Binomial[n, k]，它遵循版本 8 中开始的上述约定。变体 [n,m] 保留了帕斯卡恒等式

[n,k]=[n-1,k]+[n-1,k-1],
(7)

因此对于负整数 n 值不同，在 Wolfram 语言 中实现为PascalBinomial[n, k]。

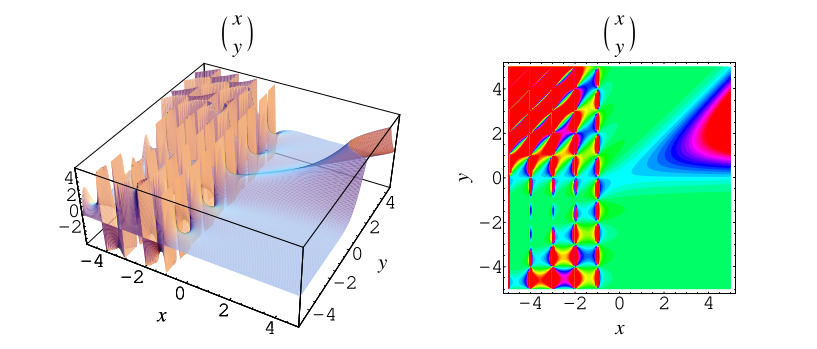
BinomialCoefficient

在 xy 平面上绘制二项式系数（Fowler 1996）给出了上面所示的漂亮图表，对于 负数 x 和 y，它有一个非常复杂的图形，因此很难使用标准绘图程序渲染。

对于正整数 n，二项式定理给出

(x+a)^n=sum_(k=0)^n(n; k)x^ka^(n-k).
(8)

这个恒等式的有限差分模拟被称为 朱-范德蒙恒等式。类似的公式对于负整数也成立，

(x+a)^(-n)=sum_(k=0)^infty(-n; k)x^ka^(-n-k).
(9)

有许多优雅的二项式和。

二项式系数满足以下恒等式

(n; 0)=(n; n)=1
(10)
(n; k)=(n; n-k)
(11)
(n; k+1)=(n; k)(n-k)/(k+1)
(12)
(n+1; k)=(n; k)+(n; k-1).
(13)

二项式系数的乘积由下式给出

product_(k=0)^n(n; k)=(H^2(n))/((n!)^(n+1)),
(14)

其中 H(n) 是一个 超阶乘，n! 是一个 阶乘。

正如库默在 1852 年表明的那样，如果 p^k 是素数 p 的最大幂，它能整除 (m+n; m)，其中 m 和 n 是非负整数，那么 k 是在以 p 为基数将 m 加到 n 时发生的进位数 (Graham et al. 1989, Exercise 5.36, p. 245; Ribenboim 1989; Vardi 1991, p. 68)。库默的结果也可以用另一种形式表示：素数 p 除以 (n; m) 的指数由整数 j>=0 的数量给出，对于这些整数

frac(m/p^j)>frac(n/p^j),
(15)

其中 frac(x) 表示 x 的小数部分。这个不等式可以简化为对指数和 sum_(n)Lambda(n)e(x/n) 的研究，其中 Lambda(n) 是 芒戈尔特函数。Jutila (1973, 1974) 给出了这些和的估计，但 Granville 和 Ramare (1996) 进行了最新的改进。

R. W. Gosper 表明

f(n)=(n-1; 1/2(n-1))=(-1)^((n-1)/2) (mod n)
(16)

对于所有素数都成立，并推测它仅对素数成立。当 Skiena (1990) 发现它也适用于合数 n=3×11×179 时，这个推测被推翻。Vardi (1991, p. 63) 随后表明，当 p 是维费里希素数 时，n=p^2 是一个解，并且如果 n=p^k 且 k>3 是一个解，那么 n=p^(k-1) 也是一个解。这使他能够证明，对于合数 n<1.3×10^7，唯一的解是 5907、1093^2 和 3511^2，其中 1093 和 3511 是 维费里希素数。

考虑二项式系数 f(n)=(2n-1; n)，前几个系数为 1, 3, 10, 35, 126, ... (OEIS A001700)。生成函数为

1/2[1/(sqrt(1-4x))-1]=x+3x^2+10x^3+35x^4+....
(17)

这些数字仅对于 n=2, 3, 4, 6, 9, 10, 12, 36, ... (OEIS A046097) 是无平方因子的，目前尚不清楚是否有其他值。事实证明，除非 n 属于 2-自动集 S_2，否则 f(n) 可被 4 整除，而 2-自动集 S_2 恰好是 二进制 表示最多包含两个 1 的数字集合：1, 2, 3, 4, 5, 6, 8, 9, 10, 12, 16, 17, 18, ... (OEIS A048645)。类似地，除非 n 属于 3-自动集 S_3，否则 f(n) 可被 9 整除，3-自动集 S_3 由数字 n 组成，对于这些数字，三进制 中 2n 的表示完全由 0 和 2 组成（除非可能有一对相邻的 1）。S_3 的初始元素是 1, 2, 3, 4, 6, 7, 9, 10, 11, 12, 13, 18, 19, 21, 22, 27, ... (OEIS A051382)。如果 f(n) 是无平方因子的，那么 n 必须属于 S=S_2 intersection S_3。很可能 S 是有穷的，但尚无证明。现在，大于 4 和 9 的平方数也可能整除 f(n)，但仅通过排除这两个，对于 n 来说，n<=2^(64) 的唯一可能值是 1, 2, 3, 4, 6, 9, 10, 12, 18, 33, 34, 36, 40, 64, 66, 192, 256, 264, 272, 513, 514, 516, 576 768, 1026, 1056, 2304, 16392, 65664, 81920, 532480 和 545259520。除了最后一个，所有这些都已检查过，证实对于 n<=545259520，没有其他 n 使 f(n) 是无平方因子的。

Erdős 表明，对于 3<=k<=n/2，二项式系数 (n; k) 是一个 整数 的幂，仅在 (50; 3)=140^2 一种情况下成立 (Le Lionnais 1983, p. 48)。当 a^2 是三角形数时，二项式系数 T_(n-1)=(n; 2) 是平方数 a^2，这发生在 a=1, 6, 35, 204, 1189, 6930, ... (OEIS A001109) 时。这些 a 值对应的 n=2, 9, 50, 289, 1682, 9801, ... (OEIS A052436) 值。

二项式系数 (n; |_n/2_|) 被称为中心二项式系数，其中 |_x_| 是向下取整函数，尽管系数子集 (2n; n) 有时也使用这个名称。Erdős 和 Graham (1980, p. 71) 推测，对于 n>4，中心二项式系数 (2n; n) 永远不是无平方因子的，这有时被称为埃尔德什无平方因子猜想。萨克孜定理 (Sárkőzy 1985) 提供了一个部分解，指出对于所有足够大的 n>=n_0，二项式系数 (2n; n) 永远不是无平方因子的 (Vardi 1991)。Granville 和 Ramare (1996) 证明了唯一的无平方因子值是 n=2 和 4。Sander (1992) 随后表明，只要 d 不是“太大”，对于足够大的 n，(2n+/-d; n) 也永远不是无平方因子的。

对于 p、q 和 r 个不同的素数，函数 (◇) 满足

f(pqr)f(p)f(q)f(r)=f(pq)f(pr)f(qr) (mod pqr)
(18)

(Vardi 1991, p. 66)。

大多数 n>=2k 的二项式系数 (n; k) 都有一个素因子 p<=n/k，Lacampagne et al. (1993) 推测这个不等式对于所有 n>17.125k 都成立，或者更强地说，任何这样的二项式系数的最小素因子为 p<=n/k 或 p<=17，但有例外 (62; 6), (959; 56), (474; 66), (284; 28)，对于这些例外，p=19, 19, 23, 29 (Guy 1994, p. 84)。

二项式系数 (m; n) (mod 2) 可以使用异或运算 n XOR m 计算，使得 mod 2 的帕斯卡三角形非常容易构造。

Sondow (2005) 和 Sondow 与 Zudilin (2006) 注意到不等式

1/(4rm)[((r+1)^(r+1))/(r^r)]^m<((r+1)m; m)<[((r+1)^(r+1))/(r^r)]^m
(19)

对于 m 为正整数，r>=1 为实数。

另请参阅

Apéry 数, 平衡二项式系数, 投票问题, 伯努利三角形, 二项式, 二项分布, 二项式恒等式, 二项式和, 二项式定理, 中心二项式系数, 选择, 圣诞袜定理, 朱-范德蒙恒等式, 组合, 亏量, 埃尔德什无平方因子猜想, 例外二项式系数, 阶乘, Fibonomial 系数, 伽玛函数, 良好二项式系数, k-子集, 国王问题, Klee 恒等式, Lah 数, 多重选择, 多项式系数, 帕斯卡公式, 排列, q-二项式系数, 罗马系数, 萨克孜定理, Stanley 恒等式, 大卫之星定理, Stolarsky-Harborth 常数, Strehl 恒等式, Székely 恒等式, Wolstenholme 定理 在 MathWorld 课堂中探索此主题

相关 Wolfram 网站

http://functions.wolfram.com/GammaBetaErf/Binomial/

使用 Wolfram|Alpha 探索

参考文献

Abramowitz, M. 和 Stegun, I. A. (Eds.). "二项式系数." §24.1.1 in 数学函数手册，包含公式、图形和数学表格，第 9 次印刷。 New York: Dover, pp. 10, 256, 和 822-823, 1972.Comtet, L. 高级组合数学：有限与无限展开的艺术，修订和扩充版。 Dordrecht, Netherlands: Reidel, 1974.Conway, J. H. 和 Guy, R. K. In 数字之书。 New York: Springer-Verlag, pp. 66-74, 1996.Erdős, P.; Graham, R. L.; Nathanson, M. B.; 和 Jia, X. 组合数论中的新旧问题和结果。 New York: Springer-Verlag, 1998.Erdős, P.; Lacampagne, C. B.; 和 Selfridge, J. L. "二项式系数的最小素因子估计." Math. Comput. 61, 215-224, 1993.Feller, W. "二项式系数" 和 "涉及二项式系数的问题和恒等式." §2.8 和 2.12 in 概率论及其应用导论，第 1 卷，第 3 版。 New York: Wiley, pp. 48-50 和 61-64, 1968.Fowler, D. "二项式系数函数." Amer. Math. Monthly 103, 1-17, 1996.Graham, R. L.; Knuth, D. E.; 和 Patashnik, O. "二项式系数." Ch. 5 in 具体数学：计算机科学基础。 Reading, MA: Addison-Wesley, pp. 153-242, 1989.Granville, A. "二项式系数的算术性质。I. 模素数幂的二项式系数." In 有机数学。1995 年 12 月 12-14 日在 BC 省伯纳比举行的研讨会论文集 (Ed. J. Borwein, P. Borwein, L. Jörgenson 和 R. Corless). Providence, RI: Amer. Math. Soc., pp. 253-276, 1997.Granville, A. "二项式系数的算术性质." http://www.dms.umontreal.ca/~andrew/Binomial/.Granville, A. 和 Ramaré, O. "指数和的显式界限和无平方因子二项式系数的稀缺性." Mathematika 43, 73-107, 1996.Guy, R. K. "二项式系数", "二项式系数的最大除数", 和 "与 zeta-函数相关的级数." §B31, B33, 和 F17 in 数论中未解决的问题，第 2 版。 New York: Springer-Verlag, pp. 84-85, 87-89, 和 257-258, 1994.Harborth, H. "奇数二项式系数的数量." Not. Amer. Math. Soc. 23, 4, 1976.Hilton, P. 和 Pedersen, J. "卡特兰数、它们的推广及其应用." Math. Intel. 13, 64-75, 1991.Jutila, M. "具有大素因子的数." J. Indian Math. Soc. 37, 43-53, 1973.Jutila, M. "具有大素因子的数. II." J. Indian Math. Soc. 38, 125-130, 1974.Kronenburg, M. "负参数的二项式系数." 2011 年 5 月 18 日. http://arxiv.org/abs/1105.3689/.Le Lionnais, F. 卓越的数字。 Paris: Hermann, 1983.Loeb, D. E. "二项式系数的推广." 1995 年 2 月 9 日. http://arxiv.org/abs/math/9502218.Ogilvy, C. S. "二项式系数." Amer. Math. Monthly 57, 551-552, 1950.Press, W. H.; Flannery, B. P.; Teukolsky, S. A.; 和 Vetterling, W. T. "伽玛函数、贝塔函数、阶乘、二项式系数." §6.1 in FORTRAN 数值食谱：科学计算的艺术，第 2 版。 Cambridge, England: Cambridge University Press, pp. 206-209, 1992.Prudnikov, A. P.; Marichev, O. I.; 和 Brychkow, Yu. A. 公式 41 in 积分与级数，第 1 卷：初等函数。 Newark, NJ: Gordon & Breach, p. 611, 1986.Ribenboim, P. 素数记录新书。 New York: Springer-Verlag, pp. 23-24, 1989.Riordan, J. "逆关系和组合恒等式." Amer. Math. Monthly 71, 485-498, 1964.Roman, S. "对数二项式公式." Amer. Math. Monthly 99, 641-648, 1992.Sander, J. W. "二项式系数的素因子." Bull. London Math. Soc. 24, 140-142, 1992.Sárkőzy, A. "关于二项式系数的除数，I." J. Number Th. 20, 70-80, 1985.Skiena, S. 实现离散数学：Mathematica 中的组合数学和图论。 Reading, MA: Addison-Wesley, p. 262, 1990.Sloane, N. J. A. 序列 A001109/M4217, A001700/M2848, A046097, A048645, A051382, 和 A052436, in "整数序列在线百科全书."Sondow, J. "问题 11132." Amer. Math. Monthly 112, 180, 2005.Sondow, J. 和 Zudilin, W. "欧拉常数、q-对数以及 Ramanujan 和 Gosper 的公式." Ramanujan J. 12, 225-244, 2006.Spanier, J. 和 Oldham, K. B. "二项式系数 (nu; m)." Ch. 6 in 函数图集。 Washington, DC: Hemisphere, pp. 43-52, 1987.Sved, M. "计数和重新计数." Math. Intel. 5, 21-26, 1983.Vardi, I. "二项式系数的应用", "二项式系数", "一类解", "计算二项式系数", 和 "模整数的二项式." §2.2, 4.1, 4.2, 4.3, 和 4.4 in Mathematica 计算娱乐。 Redwood City, CA: Addison-Wesley, pp. 25-28 和 63-71, 1991.Wolfram, S. "二项式系数的几何." Amer. Math. Monthly 91, 566-571, 1984.

Wolfram|Alpha 参考内容

二项式系数

请引用为

Weisstein, Eric W. "二项式系数." 来自 MathWorld--Wolfram Web 资源。 https://mathworld.net.cn/BinomialCoefficient.html

主题分类