主题
Search

阶乘

DOWNLOAD Mathematica Notebook下载 Wolfram Notebook

阶乘 n! 对于正整数 n 定义为

n!=n(n-1)...2·1.
(1)

因此，例如，4!=4·3·2·1=24。较旧的阶乘记号写作 FactorialOld (Mellin 1909; Lewin 1958, p. 19; Dudeney 1970; Gardner 1978; Conway and Guy 1996)。

特殊情况 0! 被定义为值 0!=1，这与恰好一个排列零个对象的组合解释一致（即，零个元素的排列只有一个，即空集 emptyset）。

阶乘在 Wolfram 语言中实现为阶乘[n] 或 n!。

三角形数 T_n=n+(n-1)+...+2+1 可以被看作是阶乘 n!=n·(n-1)...2·1 的加法模拟。阶乘和三角形数之间的另一个关系由以下恒等式给出

(2n)!=2^nproduct_(k=1)^nT_(2k-1)
(2)

(K. MacMillan，私人通信，1 月 21 日，2008 年）。

阶乘 n! 给出了 n 个对象可以排列的方式的数量。例如，3!=6，因为 {1,2,3} 的六种可能的排列是 {1,2,3}、{1,3,2}、{2,1,3}、{2,3,1}、{3,1,2}、{3,2,1}。对于 n=0、1、2、...，前几个阶乘是 1、1、2、6、24、120、... (OEIS A000142)。

对于 n=0、1、...，(10^n)! 中的位数是 1、7、158、2568、35660、456574、5565709、65657060、... (OEIS A061010)。

可以定义阶乘的推广，例如双阶乘 n!! 和多阶乘 n!...!_()_(k)。但是请注意，这些不等于嵌套阶乘 (n!)!、((n!)!)! 等。

对于 n=1、2、...，(n!)! 的前几个值是 1、2、720、620448401733239439360000、... (Eureka 1974; OEIS A000197)。(n!)! 中的位数是 1、1、3、24、199、1747、... (OEIS A063979)。

当 n 变大时，阶乘开始出现尾随零。要计算 n! 的尾随零的数量 Z，请使用

Z=sum_(k=1)^(k_(max))|_n/(5^k)_|,
(3)

其中

k_(max)=|_log_5n_|
(4)

且 |_x_| 是向下取整函数 (Gardner 1978, p. 63; Ogilvy and Anderson 1988, pp. 112-114)。对于 n=1、2、...，尾随零的数量是 0、0、0、0、1、1、1、1、1、2、2、2、2、2、3、3、... (OEIS A027868)。这是勒让德在 1808 年首次发现的一般结果的特殊应用：整除 n! 的素数 p 的最大幂是

epsilon_p(n)=sum_(k=1)^(|_log_pn_|)|_n/(p^k)_|
(5)

(Landau 1974, pp. 75-76; Honsberger 1976; Hardy and Wright 1979, pp. 342; Ribenboim 1989; Ingham 1990, p. 20; Graham et al. 1994; Vardi 1991; Hardy 1999, pp. 18 and 21; Havil 2003, p. 165; Boros and Moll 2004, p. 5)。这可以在 Wolfram 语言中实现为

  HighestPower[p_?PrimeQ, n_] :=
    Sum[Floor[n/p^k], {k, Floor[Log[p,n]]}]

换句话说，整除 n! 的素数 p 的精确幂是

(n-s_p(n))/(p-1),
(6)

其中 s_p(n) 是 n 在 b 进制下的数字和 (Boros and Moll 2004, p. 6)。这可以在 Wolfram 语言中实现为

  HighestPower2[p_Integer?PrimeQ, n_] :=
    (n - Total[IntegerDigits[n, p]])/(p - 1)

因此，正如勒让德所示，

n!=product_(p<=n)p^(epsilon_p(n))
(7)

(Havil 2003, p. 165)。

设 a(n) 为 n! 中的最后一个非零数字，则前几个值是 2、6、4、2、2、4、2、8、8、8、6、8、... (OEIS A008904)。Kakutani (1967) 研究了这个序列，他表明这个序列是“5-自动的”，大致意思是存在一个有限自动机，当给定 n 在 5 进制下的数字时，它将最终进入一个状态，该状态的输出映射指定 a(n)。数字的精确分布由此结果得出。

Factorial
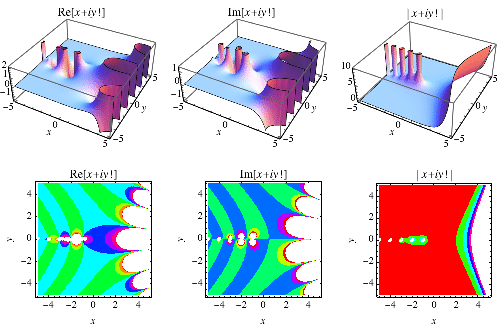FactorialReImAbs
最小值 最大值
实部
虚部 Powered by webMathematica

通过注意到

n!=Gamma(n+1),
(8)

其中 Gamma(n) 是伽玛函数，对于整数 n，定义可以推广到复数值

z!=Gamma(z+1)=int_0^inftye^(-t)t^zdt.
(9)

这定义了所有复数值 z 的 z!，除非 n 是负整数，在这种情况下，n! 等于复无穷大。

虽然高斯 (G1) 引入了记号

Pi(s)=Gamma(s+1),
(10)

但在勒让德引入伽玛记号后，此记号随后被弃用 (Edwards 2001, p. 8)。

使用伽玛函数的恒等式，(1/2n)!（半整数值）的值可以显式写出

(-1/2)!=sqrt(pi)
(11)
(1/2)!=1/2sqrt(pi)
(12)
(n-1/2)!=(sqrt(pi))/(2^n)(2n-1)!!
(13)
(n+1/2)!=(sqrt(pi))/(2^(n+1))(2n+1)!!,
(14)

其中 n!! 是双阶乘。

对于整数 s 和 n，且 s<n,

((s-n)!)/((2s-2n)!)=((-1)^(n-s)(2n-2s)!)/((n-s)!).
(15)

z! 的对数经常遇到

ln(z!)=1/2ln[(piz)/(sin(piz))]-gammaz-sum_(n=1)^(infty)(zeta(2n+1))/(2n+1)z^(2n+1)
(16)
=1/2ln[(piz)/(sin(piz))]-1/2ln((1+z)/(1-z))+(1-gamma)z-sum_(n=1)^(infty)[zeta(2n+1)-1](z^(2n+1))/(2n+1)
(17)
=sum_(n=1)^(infty)(z^n)/(n!)psi_(n-1)(1)
(18)
=-gammaz+sum_(n=2)^(infty)(-1)^n(z^n)/nzeta(n)
(19)
=-ln(1+z)+z(1-gamma)+sum_(n=2)^(infty)(-1)^n[zeta(n)-1](z^n)/n,
(20)

其中 gamma 是欧拉-马歇罗尼常数，zeta(z) 是黎曼 zeta 函数，而 psi_n(z) 是多伽玛函数。

它也由极限给出

ln(z!)=ln[lim_(n->infty)(zn!)/((z)_(n+1))n^z]
(21)
=ln[lim_(n->infty)(n!)/((z+1)_n)n^z]
(22)
=ln[lim_(n->infty)(n!)/((z+1)(z+2)...(z+n))n^z]
(23)
=lim_(n->infty)[ln(n!)+zlnn-ln(z+1)-ln(z+2)-...-ln(z+n)],
(24)

其中 (z)_n 是波赫哈默尔符号。

其中 gamma 是欧拉-马歇罗尼常数，zeta(z) 是黎曼 zeta 函数，而 psi_n(z) 是多伽玛函数。阶乘可以展开为级数

z!=sqrt(2pi)z^(z+1/2)e^(-z)(1+1/(12)z^(-1)+1/(288)z^(-2)-(139)/(51840)z^(-3)+...)
(25)

(OEIS A001163 和 A001164)。斯特林级数给出了 ln(z!) 的级数展开

ln(z!)=1/2ln(2pi)+(z+1/2)lnz-z+(B_2)/(2z)+...+(B_(2n))/(2n(2n-1)z^(2n-1))+...
(26)
=1/2ln(2pi)+(z+1/2)lnz-z+1/(12)z^(-1)-1/(360)z^(-3)+1/(1260)z^(-5)-...
(27)

(OEIS A046968 和 A046969)，其中 B_n 是伯努利数。

一般来说，幂乘积序列 (Mudge 1997) 由 S_k^+/-(n)=(n!)^k+/-1 给出。S_2^+(n) 的前几项是 2、5、37、577、14401、518401、... (OEIS A020549)，并且对于 n=1、2、3、4、5、9、10、11、13、24、65、76、...，S_2^+(n) 是素数 (OEIS A046029)。S_2^-(n) 的前几项是 0、3、35、575、14399、518399、... (OEIS A046032)，但 S_2^-(n) 仅对于 n=2 是素数，因为对于 n>2，S_2^-(n)=(n!)^2-1=(n!+1)(n!-1)。S_3^-(n) 的前几项是 0、7、215、13823、1727999、... (OEIS A046033)，而 S_3^+(n) 的前几项是 2、9、217、13825、1728001、... (OEIS A019514)。

前几个数 n，使得其数字的阶乘之和等于素数计数函数 pi(n) 是 6500、6501、6510、6511、6521、12066、50372、... (OEIS A049529)。此序列是有限的，最大项是 a_(23)=11071599。

满足以下条件的数 n 被称为威尔逊素数。

(n-1)!+1=0 (mod n^2),
(28)

被称为威尔逊素数。

布朗数是满足布罗卡尔问题条件的整数对 (m,n)，即满足

n!+1=m^2.
(29)

仅已知三对这样的数：(5, 4), (11, 5), (71, 7)。Erdős 猜想这仅有的三个这样的对 (Guy 1994, p. 193)。

另请参阅

Alladi-Grinstead 常数, 交错阶乘, 布罗卡尔问题, 布朗数, 中心阶乘, 双阶乘, 阶乘素数, 阶乘积, 阶乘和, Factorion, 降阶乘, Fibonorial, 伽玛函数, 超阶乘, Legions 数, Leviathan 数, 多阶乘, 波赫哈默尔符号, 素数阶乘, 升阶乘, 罗马阶乘, 斯特林级数, 次阶乘, 超超阶乘, 威尔逊素数 在 MathWorld 课堂中探索此主题

相关 Wolfram 网站

http://functions.wolfram.com/GammaBetaErf/Factorial/

使用 Wolfram|Alpha 探索

参考文献

Boros, G. 和 Moll, V. Irresistible Integrals: Symbolics, Analysis and Experiments in the Evaluation of Integrals. Cambridge, England: Cambridge University Press, 2004.Caldwell, C. K. "The Top Twenty: Primorial and Factorial Primes." http://www.utm.edu/research/primes/lists/top20/PrimorialFactorial.html.Conway, J. H. 和 Guy, R. K. "Factorial Numbers." 在 The Book of Numbers. New York: Springer-Verlag, pp. 65-66, 1996.Dudeney, H. E. Amusements in Mathematics. New York: Dover, p. 96, 1970.Edwards, H. M. "The Factorial Function." §in 1.3 Riemann's Zeta Function. New York: Dover, pp. 7-9, 2001.Gardner, M. "Factorial Oddities." Ch. 4 在 Mathematical Magic Show: More Puzzles, Games, Diversions, Illusions and Other Mathematical Sleight-of-Mind from Scientific American. New York: Vintage, pp. 50-65, 1978.Gauss, C. F. "Disquisitiones Generales Circa Seriem Infinitam [(alphabeta)/(1·gamma)]x+[(alpha(alpha+1)beta(beta+1))/(1·2·gamma(gamma+1))]x^2 +[(alpha(alpha+1)(alpha+2)beta(beta+1)(beta+2))/(1·2·3·gamma(gamma+1)(gamma+2))]x^3+ etc. Pars Prior." Commentationes Societiones Regiae Scientiarum Gottingensis Recentiores, Vol. II. 1812. Reprinted in Gesammelte Werke, Bd. 3, pp. 123-163 和 207-229, 1866.Glynn, J. 和 Gray, T. The Beginner's Guide To Mathematica, Version 4. Cambridge, England: Cambridge University Press, 2000.Graham, R. L.; Knuth, D. E.; 和 Patashnik, O. "Factorial Factors." §4.4 在 Concrete Mathematics: A Foundation for Computer Science, 2nd ed. Reading, MA: Addison-Wesley, pp. 111-115, 1994.Guy, R. K. "Equal Products of Factorials," "Alternating Sums of Factorials," 和 "Equations Involving Factorial n." §B23, B43, 和 D25 在 Unsolved Problems in Number Theory, 2nd ed. New York: Springer-Verlag, pp. 80, 100, 和 193-194, 1994.Hardy, G. H. Ramanujan: Twelve Lectures on Subjects Suggested by His Life and Work, 3rd ed. New York: Chelsea, 1999.Hardy, G. H. 和 Wright, E. M. An Introduction to the Theory of Numbers, 5th ed. Oxford, England: Clarendon Press, 1979.Havil, J. Gamma: Exploring Euler's Constant. Princeton, NJ: Princeton University Press, 2003.Hoey, D. "Re: 01 squares." [email protected] posting, May 19, 1997.Honsberger, R. Mathematical Gems II. Washington, DC: Math. Assoc. Amer., p. 2, 1976.Ingham, A. E. The Distribution of Prime Numbers. Cambridge, England: Cambridge University Press, 1990.Jeffreys, H. 和 Jeffreys, B. S. Methods of Mathematical Physics, 3rd ed. Cambridge, England: Cambridge University Press, pp. 462-463, 1988.Kakutani, S. "Ergodic Theory of Shift Transformations." 在 Proc. 5th Berkeley Symposium on Mathematical Statistics and Probability, Vol. 2. Berkeley, CA: University of California Press, pp. 405-414, 1967.Landau, E. Handbuch der Lehre von der Verteilung der Primzahlen, 3rd ed. New York: Chelsea, 1974.Lewin, L. Dilogarithms and Associated Functions. London: Macdonald, 1958.Leyland, P. http://www.leyland.vispa.com/numth/factorization/factors/factorial+.txt.Leyland, P. http://www.leyland.vispa.com/numth/factorization/factors/factorial-.txt.Madachy, J. S. Madachy's Mathematical Recreations. New York: Dover, p. 174, 1979.Mellin, H. "Abrißeiner einheitlichen Theorie der Gamma- und der hypergeometrischen Funktionen." Math. Ann. 68, 305-337, 1909.Mudge, M. "Not Numerology but Numeralogy!" Personal Computer World, 279-280, 1997.Ogilvy, C. S. 和 Anderson, J. T. Excursions in Number Theory. New York: Dover, 1988.Petkovšek, M.; Wilf, H. S.; 和 Zeilberger, D. A=B. Wellesley, MA: A K Peters, p. 86, 1996. http://www.cis.upenn.edu/~wilf/AeqB.html.Press, W. H.; Flannery, B. P.; Teukolsky, S. A.; 和 Vetterling, W. T. "Gamma Function, Beta Function, Factorials, Binomial Coefficients." §6.1 在 Numerical Recipes in FORTRAN: The Art of Scientific Computing, 2nd ed. Cambridge, England: Cambridge University Press, pp. 206-209, 1992.Ribenboim, P. The New Book of Prime Number Records. New York: Springer-Verlag, pp. 22-24, 1989.Sloane, N. J. A. 序列 A000142/M1675, A000197/M2187, A001163/M5400, A001164/M4878, A008904, A019514, A020549, A027868, A046029, A046032, A046033, A046968, A046969, A049529, A061010, 和 A063979 在 "整数序列在线百科全书" 中。Spanier, J. 和 Oldham, K. B. "The Factorial Function n! and Its Reciprocal." Ch. 2 在 An Atlas of Functions. Washington, DC: Hemisphere, pp. 19-33, 1987.Trott, M. The Mathematica GuideBook for Programming. New York: Springer-Verlag, p. 81, 2004. http://www.mathematicaguidebooks.org/.Vardi, I. Computational Recreations in Mathematica. Reading, MA: Addison-Wesley, p. 67, 1991.Vout, C. 和 Brown, M. "Problems Drive." Eureka 37, 11, 1974.

在 Wolfram|Alpha 上被引用

阶乘

请引用为

Weisstein, Eric W. "阶乘。" 来自 MathWorld--Wolfram Web 资源。 https://mathworld.net.cn/Factorial.html

主题分类