主题
Search

超阶乘

DOWNLOAD Mathematica Notebook下载 Wolfram 笔记本
Hyperfactorial

超阶乘（Sloane 和 Plouffe 1995）是由下式定义的函数

H(n)=K(n+1)
(1)
=product_(k=1)^(n)k^k,
(2)

其中 K(n) 是 K 函数。

超阶乘在 Wolfram 语言 中实现为超阶乘[n]。

对于整数值 n=1、2、... 分别为 1、4、108、27648、86400000、4031078400000、3319766398771200000、... (OEIS A002109)。

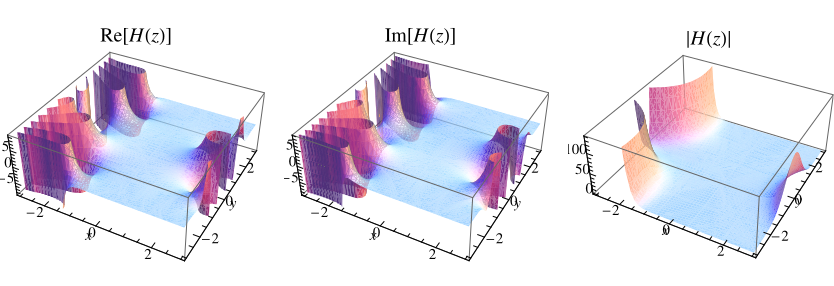
HyperfactorialReIm
HyperfactorialContours

超阶乘也可以推广到复数，如上所示。

Barnes G 函数和超阶乘 H(z) 满足以下关系

H(z-1)G(z)=e^((z-1)logGamma(z))
(3)

对于所有复数 z。

超阶乘由积分给出

H(z)=(2pi)^(-z/2)exp[(z+1; 2)+int_0^zln(t!)dt]
(4)

和闭合形式表达式

K(z)=exp[zeta^'(-1,z+1)-zeta^'(-1)]
(5)

对于 R[z]>0，其中 zeta(z) 是 黎曼 zeta 函数，zeta^'(z) 是它的导数，zeta(a,z) 是 赫尔维茨 zeta 函数，并且

zeta^'(a,z)=[(dzeta(s,z))/(ds)]_(s=a).
(6)

H(z) 也具有 斯特林 级数

H(z)∼Ae^(-z^2/4)z^(z(z+1)/2+1/12)×(1+1/(720z^2)-(1433)/(7257600z^4)+...)
(7)

（OEIS A143475 和 A143476）。

H(-1/2) 具有特殊值

H(-1/2)=e^(-[(ln2)/3+12zeta^'(-1)]/8)
(8)
=2^(1/12)pi^(1/8)e^([gamma-1-zeta^'(2)/zeta(2)]/8)
(9)
=(A^(3/2))/(2^(1/24)e^(1/8)),
(10)

其中 gamma 是 欧拉-马歇罗尼常数，A 是 格莱舍-金克林常数。

导数由下式给出

(dH(x))/(dx)=H(x){1/2[1-ln(2pi)]+ln(Gamma(x+1))+x}.
(11)

另请参阅

Barnes G 函数, 格莱舍-金克林常数, K 函数, 超阶乘

使用 Wolfram|Alpha 探索

参考文献

Fletcher, A.; Miller, J. C. P.; Rosenhead, L.; and Comrie, L. J. An Index of Mathematical Tables, Vol. 1, 2nd ed. Reading, MA: Addison-Wesley, p. 50, 1962.Graham, R. L.; Knuth, D. E.; and Patashnik, O. Concrete Mathematics: A Foundation for Computer Science, 2nd ed. Reading, MA: Addison-Wesley, p. 477, 1994.Sloane, N. J. A. Sequences A002109/M3706, A143475, and A143476 in "The On-Line Encyclopedia of Integer Sequences."

在 Wolfram|Alpha 中引用

超阶乘

请引用为

Weisstein, Eric W. "超阶乘。" 来自 MathWorld--Wolfram Web 资源。 https://mathworld.net.cn/Hyperfactorial.html

学科分类