主题
Search

伽玛函数

DOWNLOAD Mathematica Notebook下载 Wolfram 笔记本
GammaFunction

（完全）伽玛函数 Gamma(n) 被定义为 阶乘 到 复数 和 实数 变量的扩展。它与 阶乘 的关系为

Gamma(n)=(n-1)!,
(1)

勒让德引入了一个稍微不幸的符号，现在被普遍使用，而不是高斯更简单的 Pi(n)=n! (Gauss 1812; Edwards 2001, p. 8)。

除了在 z=0, -1, -2, ... 之外，它在所有地方都是 解析 的，并且在 z=-k 的留数为

Res_(z=-k)Gamma(z)=((-1)^k)/(k!).
(2)

没有 z 点使得 Gamma(z)=0。

伽玛函数在 Wolfram 语言 中实现为Gamma[z]。

对于伽玛函数的幂，有许多常用的符号惯例。虽然像 Watson (1939) 这样的作者使用 Gamma^n(z) (即，使用类似于三角函数的惯例)，但通常也写成 [Gamma(z)]^n。

伽玛函数可以定义为 R[z]>0 的 定积分 （欧拉积分形式）

Gamma(z)=int_0^inftyt^(z-1)e^(-t)dt
(3)
=2int_0^inftye^(-t^2)t^(2z-1)dt,
(4)

或

Gamma(z)=int_0^1[ln(1/t)]^(z-1)dt.
(5)

完全伽玛函数 Gamma(x) 可以推广到上 不完全伽玛函数 Gamma(a,x) 和下 不完全伽玛函数 gamma(a,x)。

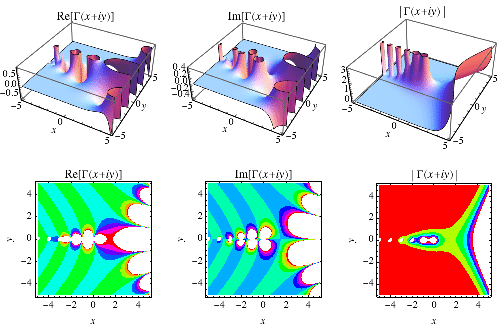GammaReImAbs
最小值 最大值
实部
虚部 Powered by webMathematica

上面展示了复平面中 Gamma(z) 的实部和虚部的图。

对于 实数 变量，通过对公式 (3) 进行分部积分，可以看出

Gamma(x)=int_0^inftyt^(x-1)e^(-t)dt
(6)
=[-t^(x-1)e^(-t)]_0^infty+int_0^infty(x-1)t^(x-2)e^(-t)dt
(7)
=(x-1)int_0^inftyt^(x-2)e^(-t)dt
(8)
=(x-1)Gamma(x-1).
(9)

如果 x 是一个 整数 n=1, 2, 3, ...，则

Gamma(n)=(n-1)Gamma(n-1)
(10)
=(n-1)(n-2)Gamma(n-2)
(11)
=(n-1)(n-2)...1
(12)
=(n-1)!,
(13)

因此，对于 正整数 变量，伽玛函数简化为 阶乘。

Gamma(z) 和 黎曼 zeta 函数 zeta(z) 之间存在一个优美的关系，由下式给出

zeta(z)Gamma(z)=int_0^infty(u^(z-1))/(e^u-1)du
(14)

对于 R[z]>1 (Havil 2003, p. 60)。

伽玛函数也可以通过 无穷乘积 形式定义 (Weierstrass 形式)

Gamma(z)=[ze^(gammaz)product_(r=1)^infty(1+z/r)e^(-z/r)]^(-1),
(15)

其中 gamma 是 欧拉-马歇罗尼常数 (Krantz 1999, p. 157; Havil 2003, p. 57)。对 (◇) 两边取对数，

-ln[Gamma(z)]=lnz+gammaz+sum_(n=1)^infty[ln(1+z/n)-z/n].
(16)

求导，

-(Gamma^'(z))/(Gamma(z))=1/z+gamma+sum_(n=1)^(infty)((1/n)/(1+z/n)-1/n)
(17)
=1/z+gamma+sum_(n=1)^(infty)(1/(n+z)-1/n)
(18)
Gamma^'(z)=-Gamma(z)[1/z+gamma+sum_(n=1)^(infty)(1/(n+z)-1/n)]
(19)
=Gamma(z)Psi(z)
(20)
=Gamma(z)psi_0(z)
(21)
Gamma^'(1)=-Gamma(1){1+gamma+[(1/2-1)+(1/3-1/2)+...+(1/(n+1)-1/n)+...]}
(22)
=-(1+gamma-1)
(23)
=-gamma
(24)
Gamma^'(n)=-Gamma(n){1/n+gamma+[(1/(1+n)-1)+(1/(2+n)-1/2)+(1/(3+n)-1/3)+...]}
(25)
=-(n-1)!(1/n+gamma-sum_(k=1)^(n)1/k),
(26)

其中 Psi(z) 是 双伽玛函数，psi_0(z) 是 多伽玛函数。 n 阶导数以 多伽玛函数 psi_n, psi_(n-1), ..., psi_0 的形式给出。

实数 正 x=x_0 的 Gamma(x) 的最小值 x_0 在以下情况下达到

Gamma^'(x_0)=Gamma(x_0)psi_0(x_0)=0
(27)
psi_0(x_0)=0.
(28)

这可以通过数值求解得到 x_0=1.46163... (OEIS A030169; Wrench 1968)，其 连分数 为 [1, 2, 6, 63, 135, 1, 1, 1, 1, 4, 1, 38, ...] (OEIS A030170)。在 x_0 处，Gamma(x_0) 达到值 0.8856031944... (OEIS A030171)，其 连分数 为 [0, 1, 7, 1, 2, 1, 6, 1, 1, ...] (OEIS A030172)。

欧拉极限形式为

Gamma(z)=1/zproduct_(n=1)^infty[(1+1/n)^z(1+z/n)^(-1)],
(29)

所以

Gamma(z)=lim_(n->infty)((n+1)^z)/(z(1+z)(1+z/2)(1+z/3)...(1+z/n))
(30)
=lim_(n->infty)((n+1)^zn!)/(z(z+1)(z+2)(z+3)...(z+n))
(31)
=lim_(n->infty)(n!)/((z)_(n+1))(n+1)^z
(32)
=lim_(n->infty)(n!)/((z)_(n+1))n^z
(33)

(Krantz 1999, p. 156)。

伽玛函数的倒数 1/Gamma(z) 是一个 整函数，可以表示为

1/(Gamma(z))=zexp[gammaz-sum_(k=2)^infty((-1)^kzeta(k)z^k)/k],
(34)

其中 gamma 是 欧拉-马歇罗尼常数，zeta(z) 是 黎曼 zeta 函数 (Wrench 1968)。 1/Gamma(z) 的 渐近级数 由下式给出

1/(Gamma(z))∼z+gammaz^2+1/(12)(6gamma^2-pi^2)z^3+1/(12)[2gamma^3-gammapi^2+4zeta(3)]z^4+....
(35)

写作

1/(Gamma(z))=sum_(k=1)^inftya_kz^k,
(36)

a_k 满足

a_n=na_1a_n-a_2a_(n-1)+sum_(k=2)^n(-1)^kzeta(k)a_(n-k)
(37)

(Bourguet 1883, Davis 1933, Isaacson and Salzer 1943, Wrench 1968)。Wrench (1968) 数值计算了以下函数在 0 附近的级数展开的系数

1/(z(1+z)Gamma(z))=1+(gamma-1)z+[1+1/2(gamma-2)gamma-1/(12)pi^2]z^2+....
(38)

Lanczos 近似 给出了 Gamma(z+1) 对于 z>0 的级数展开，以任意常数 sigma 表示，使得 R[z+sigma+1/2]>0。

伽玛函数满足以下 函数方程

Gamma(1+z)=zGamma(z)
(39)
Gamma(1-z)=-zGamma(-z).
(40)

其他恒等式为

Gamma(x)Gamma(-x)=-pi/(xsin(pix))
(41)
Gamma(x)Gamma(1-x)=pi/(sin(pix))
(42)
|(ix)!|^2=(pix)/(sinh(pix))
(43)
|(n+ix)!|=sqrt((pix)/(sinh(pix)))product_(s=1)^(n)sqrt(s^2+x^2).
(44)

使用 (41)，有理数 r 的伽玛函数 Gamma(r) 可以简化为一个常数乘以 Gamma(frac(r)) 或 1/Gamma(frac(r))。例如，

Gamma(2/3)=(2pi)/(sqrt(3)Gamma(1/3))
(45)
Gamma(3/4)=(sqrt(2)pi)/(Gamma(1/4))
(46)
Gamma(3/5)=sqrt(2-2/(sqrt(5)))pi/(Gamma(2/5))
(47)
Gamma(4/5)=sqrt(2+2/(sqrt(5)))pi/(Gamma(1/5)).
(48)

对于 R[z]=-1/2,

|(-1/2+iy)!|^2=pi/(cosh(piy)).
(49)

变量为 2z 的伽玛函数可以使用 Legendre 倍乘公式 表示

Gamma(2z)=(2pi)^(-1/2)2^(2z-1/2)Gamma(z)Gamma(z+1/2).
(50)

变量为 3z 的伽玛函数可以使用三倍公式表示

Gamma(3z)=(2pi)^(-1)3^(3z-1/2)Gamma(z)Gamma(z+1/3)Gamma(z+2/3).
(51)

一般结果是 Gauss 乘法公式

Gamma(z)Gamma(z+1/n)...Gamma(z+(n-1)/n)=(2pi)^((n-1)/2)n^(1/2-nz)Gamma(nz).
(52)

伽玛函数也通过下式与 黎曼 zeta 函数 zeta(z) 相关

Gamma(s/2)pi^(-s/2)zeta(s)=Gamma((1-s)/2)pi^(-(1-s)/2)zeta(1-s).
(53)

对于整数 n=1, 2, ...，Gamma(n) 的前几个值为 1, 1, 2, 6, 24, 120, 720, 5040, 40320, 362880, ... (OEIS A000142)。对于半整数变量，Gamma(n/2) 具有特殊形式

Gamma(1/2n)=((n-2)!!sqrt(pi))/(2^((n-1)/2)),
(54)

其中 n!! 是 双阶乘。n=1, 3, 5, ... 的前几个值因此为

Gamma(1/2)=sqrt(pi)
(55)
Gamma(3/2)=1/2sqrt(pi)
(56)
Gamma(5/2)=3/4sqrt(pi),
(57)

15sqrt(pi)/8, 105sqrt(pi)/16, ... (OEIS A001147 和 A000079; Wells 1986, p. 40)。一般来说，对于 n 为 正整数 n=1, 2, ...

Gamma(1/2+n)=(1·3·5...(2n-1))/(2^n)sqrt(pi)
(58)
=((2n-1)!!)/(2^n)sqrt(pi)
(59)
Gamma(1/2-n)=((-1)^n2^n)/(1·3·5...(2n-1))sqrt(pi)
(60)
=((-1)^n2^n)/((2n-1)!!)sqrt(pi).
(61)

对于 Gamma(1/n)，当 n 为正整数 n>2 时，似乎不存在这种类型的简单闭式表达式。然而，Borwein 和 Zucker (1992) 给出了各种恒等式，将伽玛函数与平方根和 椭圆积分奇异值 k_n 相关联，即，椭圆模量 k_n 使得

(K^'(k_n))/(K(k_n))=sqrt(n),
(62)

其中 K(k) 是 第一类完全椭圆积分，K^'(k)=K(k^')=K(sqrt(1-k^2)) 是互补积分。M. Trott（私人通信）开发了一种算法，用于自动生成数百个这样的恒等式。

Gamma(1/3)=2^(7/9)3^(-1/12)pi^(1/3)[K(k_3)]^(1/3)
(63)
Gamma(1/4)=2pi^(1/4)[K(k_1)]^(1/2)
(64)
Gamma(1/6)=2^(-1/3)3^(1/2)pi^(-1/2)[Gamma(1/3)]^2
(65)
Gamma(1/8)Gamma(3/8)=(sqrt(2)-1)^(1/2)2^(13/4)pi^(1/2)K(k_2)
(66)
(Gamma(1/8))/(Gamma(3/8))=2(sqrt(2)+1)^(1/2)pi^(-1/4)[K(k_1)]^(1/2)
(67)
Gamma(1/(12))=2^(-1/4)3^(3/8)(sqrt(3)+1)^(1/2)pi^(-1/2)Gamma(1/4)Gamma(1/3)
(68)
Gamma(5/(12))=2^(1/4)3^(-1/8)(sqrt(3)-1)^(1/2)pi^(1/2)(Gamma(1/4))/(Gamma(1/3))
(69)
(Gamma(1/(24))Gamma((11)/(24)))/(Gamma(5/(24))Gamma(7/(24)))=sqrt(3)sqrt(2+sqrt(3))
(70)
(Gamma(1/(24))Gamma(5/(24)))/(Gamma(7/(24))Gamma((11)/(24)))=4·3^(1/4)(sqrt(3)+sqrt(2))pi^(-1/2)K(k_1)
(71)
(Gamma(1/(24))Gamma(7/(24)))/(Gamma(5/(24))Gamma((11)/(24)))=2^(25/18)3^(1/3)(sqrt(2)+1)pi^(-1/3)[K(k_3)]^(2/3)
(72)
Gamma(1/(24))Gamma(5/(24))Gamma(7/(24))Gamma((11)/(24))=384(sqrt(2)+1)(sqrt(3)-sqrt(2))(2-sqrt(3))pi[K(k_6)]^2
(73)
Gamma(1/(10))=2^(-7/10)5^(1/4)(sqrt(5)+1)^(1/2)pi^(-1/2)Gamma(1/5)Gamma(2/5)
(74)
Gamma(3/(10))=2^(-3/5)(sqrt(5)-1)pi^(1/2)(Gamma(1/5))/(Gamma(2/5))
(75)
(Gamma(1/(15))Gamma(4/(15))Gamma(7/(15)))/(Gamma(2/(15)))=2·3^(1/2)5^(1/6)sin(2/(15)pi)[Gamma(1/3)]^2
(76)
(Gamma(1/(15))Gamma(2/(15))Gamma(7/(15)))/(Gamma(4/(15)))=2^2·3^(2/5)sin(1/5pi)sin(4/(15)pi)[Gamma(1/5)]^2
(77)
(Gamma(2/(15))Gamma(4/(15))Gamma(7/(15)))/(Gamma(1/(15)))=(2^(-3/2)3^(-1/5)5^(1/4)(sqrt(5)-1)^(1/2)[Gamma(2/5)]^2)/(sin(4/(15)pi))
(78)
(Gamma(1/(15))Gamma(2/(15))Gamma(4/(15)))/(Gamma(7/(15)))=60(sqrt(5)-1)sin(7/(15)pi)[K(k_(15))]^2
(79)
(Gamma(1/(20))Gamma(9/(20)))/(Gamma(3/(20))Gamma(7/(20)))=2^(-1)5^(1/4)(sqrt(5)+1)
(80)
(Gamma(1/(20))Gamma(3/(20)))/(Gamma(7/(20))Gamma(9/(20)))=2^(4/5)(10-2sqrt(5))^(1/2)pi^(-1)sin(7/(20)pi)sin(9/(20)pi)[Gamma(1/5)]^2
(81)
(Gamma(1/(20))Gamma(7/(20)))/(Gamma(3/(20))Gamma(9/(20)))=2^(3/5)(10+2sqrt(5))^(1/2)pi^(-1)sin(3/(20)pi)sin(9/(20)pi)[Gamma(2/5)]^2
(82)
Gamma(1/(20))Gamma(3/(20))Gamma(7/(20))Gamma(9/(20))=160(sqrt(5)-2)^(1/2)pi[K(k_5)]^2.
(83)

Campbell (1966, p. 31) 也给出了一些。

一些有趣的恒等式包括

product_(n=1)^(2)Gamma(1/3n)=(2pi)/(sqrt(3))
(84)
product_(n=1)^(3)Gamma(1/3n)=(2pi)/(sqrt(3))
(85)
product_(n=1)^(4)Gamma(1/3n)=(2piGamma(1/3))/(3sqrt(3))
(86)
product_(n=1)^(5)Gamma(1/3n)=8/(27)pi^2
(87)
product_(n=1)^(6)Gamma(1/3n)=8/(27)pi^2
(88)
product_(n=1)^(7)Gamma(1/3n)=(32)/(243)pi^2Gamma(1/3)
(89)
product_(n=1)^(8)Gamma(1/3n)=(640pi^3)/(2187sqrt(3)),
(90)

其中 Magnus 和 Oberhettinger (1949, p. 1) 仅给出了最后一种情况，以及

(Gamma^'(1))/(Gamma(1))-(Gamma^'(1/2))/(Gamma(1/2))=2ln2
(91)

(Magnus and Oberhettinger 1949, p. 1)。Ramanujan 也给出了一些引人入胜的恒等式

(Gamma^2(n+1))/(Gamma(n+xi+1)Gamma(n-xi+1))=product_(k=1)^infty[1+(x^2)/((n+k)^2)]
(92)
phi(m,n)phi(n,m)=(Gamma^3(m+1)Gamma^3(n+1))/(Gamma(2m+n+1)Gamma(2n+m+1)) ×(cosh[pi(m+n)sqrt(3)]-cos[pi(m-n)])/(2pi^2(m^2+mn+n^2)),
(93)

其中

phi(m,n)=product_(k=1)^infty[1+((m+n)/(k+m))^3],
(94)
product_(k=1)^infty[1+(n/k)^3]product_(k=1)^infty[1+3(n/(n+2k))^2]=(Gamma(1/2n))/(Gamma[1/2(n+1)])(cosh(pinsqrt(3))-cos(pin))/(2^(n+2)pi^(3/2)n)
(95)

(Berndt 1994)。

Ramanujan 给出了无穷级数

sum_(k=0)^infty(8k+1)[(Gamma(k+1/4))/(k!Gamma(1/4))]^4 =1+9(1/4)^4+17((1·5)/(4·8))^4+25((1·5·9)/(4·8·12))^4+... =(2^(3/2))/(sqrt(pi)[Gamma(3/4)]^2)
(96)

和

sum_(k=0)^infty(-1)^k(4k+1)[((2k-1)!!)/((2k)!!)]^5 =1-5(1/2)^5+9((1·3)/(2·4))^5-13((1·3·5)/(2·4·6))^5+... =2/([Gamma(3/4)]^4)
(97)

(Hardy 1923; Hardy 1924; Whipple 1926; Watson 1931; Bailey 1935; Hardy 1999, p. 7)。

以下 渐近级数 在概率论中偶尔有用（例如，一维随机游走）

(Gamma(J+1/2))/(Gamma(J))=sqrt(J)(1-1/(8J)+1/(128J^2)+5/(1024J^3)-(21)/(32768J^4)+...)
(98)

(OEIS A143503 和 A061549; Graham et al. 1994)。该级数还给出了 第一类斯特林数 到分数值的良好渐近推广。

长期以来人们都知道 Gamma(1/4)pi^(-1/4) 是 超越数 (Davis 1959)，Gamma(1/3) 也是 (Le Lionnais 1983; Borwein and Bailey 2003, p. 138)，并且 Chudnovsky 最近显然证明了 Gamma(1/4) 本身是 超越数 (Borwein and Bailey 2003, p. 138)。

存在有效的迭代算法来计算所有整数 k 的 Gamma(k/24) (Borwein and Bailey 2003, p. 137)。例如，Gamma(1/4)=3.6256099... (OEIS A068466) 的二次收敛迭代由定义给出

x_n=1/2(x_(n-1)^(1/2)+x_(n-1)^(-1/2))
(99)
y_n=(y_(n-1)x_(n-1)^(1/2)+x_(n-1)^(-1/2))/(y_(n-1)+1),
(100)

设置 x_0=sqrt(2) 和 y_1=2^(1/4)，然后

Gamma(1/4)=2(1+sqrt(2))^(3/4)[product_(n=1)^inftyx_n^(-1)((1+x_n)/(1+y_n))^3]^(1/4)
(101)

(Borwein and Bailey 2003, pp. 137-138)。

对于 Gamma(1/5)，尚不清楚是否存在这样的迭代 (Borwein and Borwein 1987; Borwein and Zucker 1992; Borwein and Bailey 2003, p. 138)。

另请参阅

Bailey 定理, Barnes G 函数, Binet 的斐波那契数公式, Bohr-Mollerup 定理, 双伽玛函数, Fransén-Robinson 常数 Gauss 乘法公式, 不完全伽玛函数, Knar 公式, Lambda 函数, Lanczos 近似, Legendre 倍乘公式, 对数伽玛函数, Mellin 公式, Mu 函数, Nu 函数, Pearson 函数, 多伽玛函数, 正则化伽玛函数, Stirling 级数, 超阶乘 在 MathWorld 课堂中探索此主题

相关 Wolfram 网站

http://functions.wolfram.com/GammaBetaErf/Gamma/, http://functions.wolfram.com/GammaBetaErf/LogGamma/

使用 Wolfram|Alpha 探索

参考文献

Abramowitz, M. and Stegun, I. A. (Eds.). "Gamma (Factorial) Function" and "Incomplete Gamma Function." §6.1 and 6.5 in Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, 9th printing. New York: Dover, pp. 255-258 and 260-263, 1972.Arfken, G. "The Gamma Function (Factorial Function)." Ch. 10 in Mathematical Methods for Physicists, 3rd ed. Orlando, FL: Academic Press, pp. 339-341 and 539-572, 1985.Artin, E. The Gamma Function. New York: Holt, Rinehart, and Winston, 1964.Bailey, W. N. Generalised Hypergeometric Series. Cambridge, England: Cambridge University Press, 1935.Berndt, B. C. Ramanujan's Notebooks, Part IV. New York: Springer-Verlag, pp. 334-342, 1994.Beyer, W. H. CRC Standard Mathematical Tables, 28th ed. Boca Raton, FL: CRC Press, p. 218, 1987.Borwein, J. and Bailey, D. Mathematics by Experiment: Plausible Reasoning in the 21st Century. Wellesley, MA: A K Peters, 2003.Borwein, J. and Borwein, P. B. Pi & the AGM: A Study in Analytic Number Theory and Computational Complexity. New York: Wiley, p. 6, 1987.Borwein, J. M. and Zucker, I. J. "Fast Evaluation of the Gamma Function for Small Rational Fractions Using Complete Elliptic Integrals of the First Kind." IMA J. Numerical Analysis 12, 519-526, 1992.Bourguet, L. "Sur les intégrales Eulériennes et quelques autres fonctions uniformes." Acta Math. 2, 261-295, 1883.Campbell, R. Les intégrales eulériennes et leurs applications. Paris: Dunod, 1966.Davis, H. T. Tables of the Higher Mathematical Functions. Bloomington, IN: Principia Press, 1933.Davis, P. J. "Leonhard Euler's Integral: A Historical Profile of the Gamma Function." Amer. Math. Monthly 66, 849-869, 1959.Edwards, H. M. Riemann's Zeta Function. New York: Dover, 2001.Erdélyi, A.; Magnus, W.; Oberhettinger, F.; and Tricomi, F. G. "The Gamma Function." Ch. 1 in Higher Transcendental Functions, Vol. 1. New York: Krieger, pp. 1-55, 1981.Finch, S. R. "Euler-Mascheroni Constant." §1.5 in Mathematical Constants. Cambridge, England: Cambridge University Press, pp. 28-40, 2003.Gauss, C. F. "Disquisitiones Generales Circa Seriem Infinitam [(alphabeta)/(1·gamma)]x+[(alpha(alpha+1)beta(beta+1))/(1·2·gamma(gamma+1))]x^2 +[(alpha(alpha+1)(alpha+2)beta(beta+1)(beta+2))/(1·2·3·gamma(gamma+1)(gamma+2))]x^3+ etc. Pars Prior." Commentationes Societiones Regiae Scientiarum Gottingensis Recentiores, Vol. II. 1812. Reprinted in Gesammelte Werke, Bd. 3, pp. 123-163 and 207-229, 1866.Graham, R. L.; Knuth, D. E.; and Patashnik, O. Answer to Problem 9.60 in Concrete Mathematics: A Foundation for Computer Science, 2nd ed. Reading, MA: Addison-Wesley, 1994.Hardy, G. H. "A Chapter from Ramanujan's Note-Book." Proc. Cambridge Philos. Soc. 21, 492-503, 1923.Hardy, G. H. "Some Formulae of Ramanujan." Proc. London Math. Soc. (Records of Proceedings at Meetings) 22, xii-xiii, 1924.Hardy, G. H. Ramanujan: Twelve Lectures on Subjects Suggested by His Life and Work, 3rd ed. New York: Chelsea, 1999.Havil, J. "The Gamma Function." Ch. 6 in Gamma: Exploring Euler's Constant. Princeton, NJ: Princeton University Press, pp. 53-60, 2003.Isaacson, E. and Salzer, H. E. "Mathematical Tables--Errata: 19. J. P. L. Bourget, 'Sur les intégrales Eulériennes et quelques autres fonctions uniformes,' Acta Mathematica, v. 2, 1883, pp. 261-295.' " Math. Tab. Aids Comput. 1, 124, 1943.Koepf, W. "The Gamma Function." Ch. 1 in Hypergeometric Summation: An Algorithmic Approach to Summation and Special Function Identities. Braunschweig, Germany: Vieweg, pp. 4-10, 1998.Krantz, S. G. "The Gamma and Beta Functions." §13.1 in Handbook of Complex Variables. Boston, MA: Birkhäuser, pp. 155-158, 1999.Le Lionnais, F. Les nombres remarquables. Paris: Hermann, p. 46, 1983.Magnus, W. and Oberhettinger, F. Formulas and Theorems for the Special Functions of Mathematical Physics. New York: Chelsea, 1949.Nielsen, N. "Handbuch der Theorie der Gammafunktion." Part I in Die Gammafunktion. New York: Chelsea, 1965.Press, W. H.; Flannery, B. P.; Teukolsky, S. A.; and Vetterling, W. T. "Gamma Function, Beta Function, Factorials, Binomial Coefficients" and "Incomplete Gamma Function, Error Function, Chi-Square Probability Function, Cumulative Poisson Function." §6.1 and 6.2 in Numerical Recipes in FORTRAN: The Art of Scientific Computing, 2nd ed. Cambridge, England: Cambridge University Press, pp. 206-209 and 209-214, 1992.Sloane, N. J. A. Sequences A000079/M1129, A000142/M1675, A001147/M3002, A030169, A030170, A030171, A030172, A061549, A068466, and A143503 in "The On-Line Encyclopedia of Integer Sequences."Spanier, J. and Oldham, K. B. "The Gamma Function Gamma(x)" and "The Incomplete Gamma gamma(nu;x) and Related Functions." Chs. 43 and 45 in An Atlas of Functions. Washington, DC: Hemisphere, pp. 411-421 and 435-443, 1987.Watson, G. N. "Theorems Stated by Ramanujan (XI)." J. London Math. Soc. 6, 59-65, 1931.Watson, G. N. "Three Triple Integrals." Quart. J. Math., Oxford Ser. 2 10, 266-276, 1939.Wells, D. The Penguin Dictionary of Curious and Interesting Numbers. Middlesex, England: Penguin Books, p. 40, 1986.Whipple, F. J. W. "A Fundamental Relation between Generalised Hypergeometric Series." J. London Math. Soc. 1, 138-145, 1926.Whittaker, E. T. and Watson, G. N. A Course in Modern Analysis, 4th ed. Cambridge, England: Cambridge University Press, 1990.Wrench, J. W. Jr. "Concerning Two Series for the Gamma Function." Math. Comput. 22, 617-626, 1968.

在 Wolfram|Alpha 上引用

伽玛函数

引用为

Weisstein, Eric W. "伽玛函数。" 来自 MathWorld--Wolfram Web 资源。 https://mathworld.net.cn/GammaFunction.html

主题分类