小数部分

函数 给出实数 的小数（非整数）部分。符号 有时被用来代替 （Graham 等，1994，第 70 页；Havil 2003，第 109 页），但由于可能与包含元素 的集合混淆，因此本作品中未使用此符号。

遗憾的是，对于 的 的含义没有普遍的共识，并且有两个常见的定义。设 为向下取整函数，则 Wolfram 语言命令FractionalPart[x] 定义为

(1)

（左图）。这个定义的好处是 ，其中 是 的整数部分。虽然 Spanier 和 Oldham (1987) 使用与 Wolfram 语言相同的定义，但他们只是非常简短地提到了这个公式，然后表示不会进一步使用。Graham 等 (1994，第 70 页)，以及也许大多数其他数学家，使用不同的定义

(2)

（右图）。

最小值 最大值 Re Im

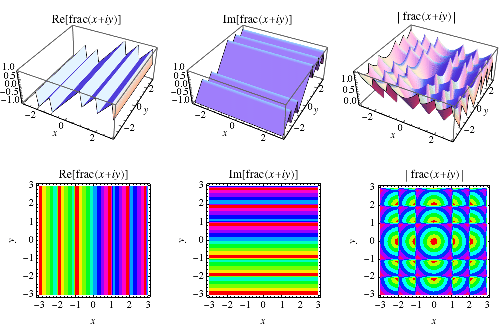小数部分函数也可以扩展到复平面，定义为

(3)

如上图所示。

由于关于小数部分/值和整数部分/值的用法可能会令人困惑，下表总结了使用的名称和符号。这里，S&O 指的是 Spanier 和 Oldham (1987)。

符号	名称	S&O	Graham 等人	Wolfram 语言
	天花板函数	--	天花板, 最小整数	Ceiling[x]
	同余	--	--	Mod[m, n]
	地板函数		地板, 最大整数, 整数部分	Floor[x]
	小数值		小数部分或	SawtoothWave[x]
	小数部分		无名称	FractionalPart[x]
	整数部分		无名称	IntegerPart[x]
	最近整数函数	--	--	Round[x]
	商	--	--	Quotient[m, n]

与后一个定义相对应的（可能缩放的）周期性波形被称为锯齿波。

上面所示的 的小数部分具有有趣的解析积分

			(4)
			(5)
			(6)
			(7)
			(8)
			(9)

积分

(10)

因此是由下式给出的伸缩和

			(11)
			(12)
			(13)

其中 是欧拉-马歇罗尼常数， 是调和数。

另一个可以用闭合形式完成并给出相同结果的相关积分是

(14)

（Havil 2003, pp. 109-111）。

上面的图显示了 在 范围内的小数部分，显示了特征间隙（Trott 2004，p. 223）。

Weyl 准则的一个结果是，对于无理数 ，序列 在区间 内是稠密的且等分布的，其中 , 2, ... (Finch 2003)。