幂

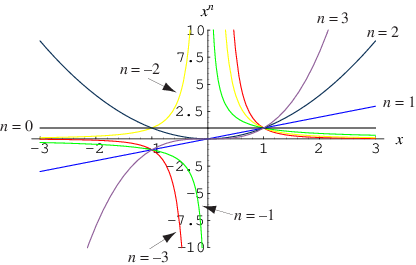
幂是指给定量的指数。表达式 因此被称为“ 的 次幂。” 上面绘制了一些 的幂（参见 Derbyshire 2004，第 68 页和 73 页）。

幂可以是整数、实数 或 复数。然而，实数的非整数次幂不一定是实数本身。例如， 仅当 时为实数。

任何非 0 的数取 0 次幂都被定义为 1，这从 极限

(1)

这一事实通过上图中曲线在 处的收敛来展示，该图显示了 ，其中 , 0.4, ..., 2.0。通过注意到重复对一个数 开 平方根 会得到越来越小的数，这些数从上方接近 1，而对 0 和 1 之间的数执行相同的操作会得到越来越大的数，这些数从下方接近 1，也可以更直观地看到这一点。对于 次平方根，总幂为 ，当 很大时，它趋近于 0，在 很大的极限情况下，得到 。

（零 的零次幂）本身是未定义的。对于这个量缺乏明确定义的含义，是由于相互矛盾的事实： 始终为 1，因此 应等于 1，但 始终为 0（对于 ），因此 应等于 0。对于 的定义通常被定义为 不定式，尽管定义 可以简化某些公式的表达（Knuth 1992；Knuth 1997，第 57 页）。

一个数的 1 次幂，根据定义，等于它本身，即

(2)

类似地，

(3)

对于任何复数 。因此，柯克舰长（威廉·夏特纳饰）能够检测到星舰企业号上比通过放大“1 的 4 次幂”的听觉传感器所能解释的心跳多一次，这令人印象深刻，这发生在第一季星际迷航剧集“军事法庭”（1967 年）中。

组合包含幂的量的规则称为 指数定律，将底数提升到给定幂的过程称为 求幂。

的 导数 由下式给出

(4)

而 不定积分 由下式给出

(5)

对于实数 的 定积分 被称为 卡瓦列里求积公式，由下式给出

(6)

虽然简单的方程

(7)

无法使用传统的 初等函数 求解 ，但可以使用 Lambert W 函数 给出解，即

(8)

其中 是 的 自然对数。

类似地，方程

(9)

可以使用 Lambert W 函数 求解 ，以 表示。在特殊情况 中，除了解 和 外，第三个解是

			(10)
			(11)

（OEIS A073084）。

下表列出了各种幂的特殊名称。

幂	名称
	倒数
	平方根
	立方根
1	恒等函数
2	平方
3	立方

形式为 的表达式被称为 幂塔。

数字 , 2, 3, ... 可以表示为 形式的最大幂 分别为 1, 1, 1, 2, 1, 1, 1, 3, 2, 1, ... (OEIS A052409)，对应的 值分别为 1, 2, 3, 2, 5, 6, 7, 2, 3, 10, ... (OEIS A052410)。

双二项式和给出幂函数如下，

(12)

（K. MacMillan，私人通信，2007 年 11 月 14 日）。

前 个 正整数 的 幂和 由 法乌尔哈伯公式 给出，

(13)

其中 是 克罗内克 delta， 是 二项式系数，而 是 伯努利数。

设 是不能表示为不同的 次 正 整数 的 和 的最大 整数 (Guy 1994)。, 3, ... 的前几个值是 128, 12758, 5134240, 67898771, ... (OEIS A001661)。

卡塔兰猜想（现在是一个定理）指出 8 和 9 ( 和 ) 是仅有的连续幂（不包括 0 和 1），即 卡塔兰丢番图问题 的唯一解。此外，Hyyrő 和 Makowski 证明不存在三个连续的幂 (Ribenboim 1996)。

很少有 形式为 的数是 素数（其中复合幂 不需要考虑，因为 ）。对于 和 素数 ，形式为 的唯一 素数 对应于 和 梅森素数，即 、、、...。形式为 的其他数等于 。对于 和 素数 ，形式为 的唯一 素数 对应于 ，其中 , 2, 4, 6, 10, 14, 16, 20, 24, 26, ... (OEIS A005574)。形式为 的其他数等于 。

方程

(14)

对于 没有非平凡解 (Guy 1994, p. 153)。