双曲正弦定义为
 |
(1)
|
符号  有时也被使用 (Gradshteyn and Ryzhik 2000, p. xxix)。它在 Wolfram 语言 中被实现为Sinh[z].
有时也被使用 (Gradshteyn and Ryzhik 2000, p. xxix)。它在 Wolfram 语言 中被实现为Sinh[z].
特殊值包括
其中  是 黄金比例。
是 黄金比例。
值
 |
(4)
|
(OEIS A073742) 具有 Engel 展开式 1, 6, 20, 42, 72, 110, ... (OEIS A068377),其闭合形式为  对于
对于  。
。
导数 由下式给出
 |
(5)
|
其中  是 双曲余弦,不定积分 由下式给出
是 双曲余弦,不定积分 由下式给出
 |
(6)
|
其中  是 积分常数。
是 积分常数。
 具有 泰勒级数
具有 泰勒级数
(OEIS A009445)。
另请参阅
Beta 指数函数,
双极坐标,
双极柱坐标,
双球坐标,
悬链线,
悬链面,
圆锥函数,
三次方程,
棣莫弗恒等式,
Dixon-Ferrar 公式,
椭圆柱坐标,
Elsasser 函数,
古德曼函数,
螺旋面,
亥姆霍兹微分方程——椭圆柱坐标,
双曲余割,
双曲函数,
反双曲正弦,
拉普拉斯方程——双球坐标,
拉普拉斯方程——环面坐标,
Lebesgue 常数,
洛伦兹群,
墨卡托投影,
米勒圆柱投影,
第二类修正贝塞尔函数,
第一类修正球贝塞尔函数,
修正斯特鲁夫函数,
Nicholson 公式,
扁球面坐标,
抛物线渐屈线,
分割函数 P,
Poinsot 螺线,
长球面坐标,
Schläfli 公式,
Shi,
正弦,
Sine-Gordon 方程,
旋转曲面,
Tau 函数,
环面坐标,
环面函数,
曳物线,
Watson 公式
使用 探索
参考文献
Abramowitz, M. 和 Stegun, I. A. (编辑)。 "双曲函数。" §4.5 在 数学函数手册,包含公式、图表和数学表格,第 9 版。 纽约:Dover,pp. 83-86, 1972。Gradshteyn, I. S. 和 Ryzhik, I. M. 积分表、级数和乘积表,第 6 版。 圣地亚哥,加利福尼亚州:Academic Press,2000。Jeffrey, A. "双曲恒等式。" §2.5 在 数学公式和积分手册,第 2 版。 奥兰多,佛罗里达州:Academic Press,pp. 117-122, 2000。Sloane, N. J. A. 整数序列 A009445, A068377, 和 A073742 在 "整数序列在线百科全书" 中。Spanier, J. 和 Oldham, K. B. "双曲正弦  和余弦
和余弦  函数。" 第 28 章 在 函数图集。 华盛顿特区:Hemisphere,pp. 263-271, 1987。Zwillinger, D. (编辑)。 "双曲函数。" §6.7 在 CRC 标准数学表格和公式。 博卡拉顿,佛罗里达州:CRC Press,pp. 476-481 1995。
函数。" 第 28 章 在 函数图集。 华盛顿特区:Hemisphere,pp. 263-271, 1987。Zwillinger, D. (编辑)。 "双曲函数。" §6.7 在 CRC 标准数学表格和公式。 博卡拉顿,佛罗里达州:CRC Press,pp. 476-481 1995。在 上被引用
双曲正弦
引用为
Weisstein, Eric W. "双曲正弦。" 来自 —— 资源。 https://mathworld.net.cn/HyperbolicSine.html
主题分类
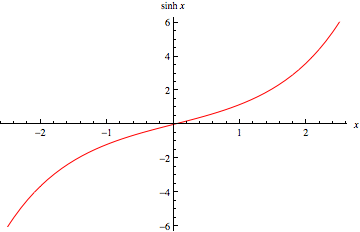
有时也被使用 (Gradshteyn and Ryzhik 2000, p. xxix)。它在 Wolfram 语言 中被实现为Sinh[z].
是 黄金比例。
对于
。
是 积分常数。
具有 泰勒级数
