主題
Search

正弦

下載 Mathematica Notebook下載 Wolfram 筆記本
Trigonometry
Sin

正弦函數 sinx 是在 三角學 中遇到的基本函數之一（其他的有 餘割、餘弦、餘切、正割 和 正切）。設 theta 為從 x 軸 沿著 弧 在 單位圓 上逆時針測量的 角。那麼 sintheta 是弧端點的垂直坐標，如上左圖所示。

SineDiagram

在 直角三角形 中，角度 theta 的正弦的常見教科書定義（與剛才給出的定義等效）是三角形中角對邊的長度與 斜邊 的長度之比，即：

sintheta=(opposite)/(hypotenuse).
(1)

一個方便記憶正弦定義以及 餘弦 和 正切 的助記符是 SOHCAHTOA（正弦等於對邊除以斜邊，餘弦 等於鄰邊除以斜邊，正切 等於對邊除以鄰邊）。

由於其定義，正弦函數是週期函數，週期為 2pi。根據 畢氏定理，sintheta 也服從恆等式

sin^2theta+cos^2theta=1.
(2)
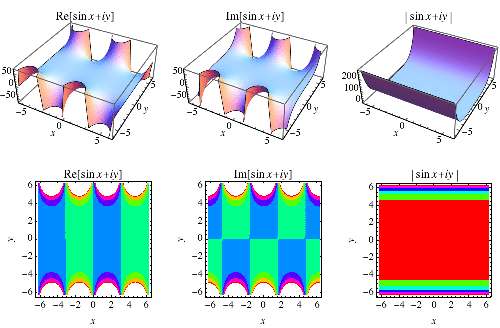SinReImAbs
最小值 最大值
實部
虛部 Powered by webMathematica

正弦函數的定義可以擴展到複數參數 z，如上圖所示，使用定義

sinz=(e^(iz)-e^(-iz))/(2i)
(3)
=1/2i(e^(-iz)-e^(iz)),
(4)

其中 e 是 自然對數 的底數，i 是 虛數單位。正弦是一個 整函數，並在 Wolfram 語言 中實現為Sin[z]。

一個相關的函數稱為 雙曲正弦，其定義類似，

sinhz=1/2(e^z-e^(-z)).
(5)

正弦函數可以通過無窮級數分析地定義為

sinx=sum_(n=1)^infty((-1)^(n-1))/((2n-1)!)x^(2n-1).
(6)

它也由複指數的 虛部 給出

sinx=I[e^(ix)].
(7)

正弦函數的乘法逆是 餘割，定義為

cscx=1/(sinx).
(8)

正弦函數也由極限給出

sin(z)=-pilim_(n->infty)1/(lnn)sum_(k=1)^infty(mu(k))/kln(n/k)frac((kz)/(2pi)),
(9)

其中 mu(k) 是 梅比烏斯函數，frac(x) 是 小數部分 (M. Trott)。

導數 sinx 是

d/(dx)sinx=cosx,
(10)

其 不定積分 是

intsinxdx=-cosx+C,
(11)

其中 C 是 積分常數。

使用來自 指數和公式 的結果

sum_(n=0)^(N)sin(nx)=I[sum_(n=0)^(N)e^(inx)]
(12)
=I[(e^(i(N+1)x)-1)/(e^(ix)-1)]
(13)
=I[(e^(i(N+1)x/2))/(e^(ix/2))(e^(i(N+1)x/2)-e^(-i(N+1)x/2))/(e^(ix/2)-e^(-ix/2))]
(14)
=(sin(1/2(N+1)x))/(sin(1/2x))I[e^(iNx/2)]
(15)
=(sin(1/2Nx)sin[1/2(N+1)x])/(sin(1/2x)).
(16)

類似地，

sum_(n=0)^(infty)p^nsin(nx)=I[sum_(n=0)^(infty)p^ne^(inx)]
(17)
=I[(1-pe^(-ix))/(1-2pcosx+p^2)]
(18)
=(psinx)/(1-2pcosx+p^2).
(19)

sin^2(kx) 的和也可以用封閉形式表示，

sum_(k=0)^Nsin^2(kx)=1/4{1+2N-cscxsin[x(1+2N)]}.
(20)

一個相關的和恆等式由下式給出

sum_(k=1)^(n-1)sin((kpi)/n)=cot(pi/(2n))
(21)

（T. Drane，私人通訊，2006 年 4 月 19 日）。

乘積恆等式包括

pisproduct_(n=1)^infty(1-(s^2)/(n^2))=sin(pis),
(22)

它更常被寫成 sinc 函數 的恆等式，或以下形式

sinx=xproduct_(n=1)^infty(1-(x^2)/(n^2pi^2))
(23)

（Edwards 2001，第 18 和 47 頁；Borwein et al. 2004，第 5 頁）。另一個乘積公式是

product_(k=1)^(n-1)sin((kpi)/n)=2^(1-n)n
(24)

（T. Drane，私人通訊，2006 年 4 月 19 日）。

正弦函數服從恆等式

sin(ntheta)=2costhetasin[(n-1)theta]-sin[(n-2)theta]
(25)

和 多倍角公式

sin(nx)=sum_(k=0)^n(n; k)cos^kxsin^(n-k)xsin[1/2(n-k)pi],
(26)

其中 (n; k) 是 二項式係數。它通過以下方式與 tan(x/2) 相關

sinx=(2tan(1/2x))/(1+tan^2(1/2x))
(27)

（Trott 2006，第 39 頁）。

一個奇特的恆等式由下式給出

(sin(nalpha))/(sinalpha)=sum_(j=1)^nproduct_(k=1; k!=j)^n(sin(alpha+theta_j-theta_k))/(sin(theta_j-theta_k))
(28)

對於所有 alpha 和 theta_j!=theta_k （Calogero 1999；Beylkin 和 Mohlenkamp 2002；Trott 2005，第 5-6 頁）。

Cvijović 和 Klinowski (1995) 表明，和

S_nu(alpha)=sum_(k=0)^infty(sin(2k+1)alpha)/((2k+1)^nu)
(29)

對於 nu=2n+1,

S_(2n+1)(alpha)=((-1)^n)/(4(2n)!)pi^(2n+1)E_(2n)(alpha/pi),
(30)

具有封閉形式，其中 E_n(x) 是 歐拉多項式。

sinx 的 連分數 表示為

sinx=x/(1+(x^2)/((2·3-x^2)+(2·3x^2)/((4·5-x^2)+(4·5x^2)/((6·7-x^2)+...))))
(31)

（Olds 1963，第 138 頁）。

對於所有整數 n>1，sin(2pi/n) 的值是 無理數，除了 2、4 和 12，對於這些值，sin(pi)=0、sin(pi/2)=1 和 sin(pi/6)=1/2 分別為 0、1 和 1/2，這個結果本質上被稱為 尼文定理。

sin(2pik_0x) 的 傅立葉變換 由下式給出

F_x[sin(2pik_0x)](k)=int_(-infty)^inftye^(-2piikx)sin(2pik_0x)dx
(32)
=1/2i[delta(k+k_0)-delta(k-k_0)].
(33)

涉及 sinx 的 定積分 由下式給出

int_0^inftysin(x^n)dx=Gamma(1+1/n)sin(pi/(2n))
(34)

對於 n>1，其中 Gamma(z) 是 伽瑪函數 (R. Mabry，私人通訊，2005 年 12 月 15 日；T. Drane，私人通訊，2006 年 4 月 21 日)。

參見

安德魯正弦、Cis、餘割、餘弦、初等函數、傅立葉變換--正弦、雙曲極正弦、雙曲正弦、超正弦、反三角函數正弦、尼文定理、極正弦、Sinc 函數、正弦曲線、SOHCAHTOA、正切、三角函數、三角學 在 課堂中探索這個主題

相關 Wolfram 網站

http://functions.wolfram.com/ElementaryFunctions/Sin/

使用 探索

參考文獻

Abramowitz, M. 和 Stegun, I. A. (編). "圓函數." §4.3 見 數學函數手冊，包含公式、圖表和數學表格，第 9 版. 紐約: Dover, pp. 71-79, 1972.Beylkin, G. 和 Mohlenkamp, M. J. Proc. Nat. Acad. Sci. USA 99, 10246, 2002.Beyer, W. H. CRC 標準數學表格，第 28 版. Boca Raton, FL: CRC Press, p. 225, 1987.Borwein, J.; Bailey, D.; 和 Girgensohn, R. 數學實驗：計算發現之路. Wellesley, MA: A K Peters, 2004.Calogero, F. "顯著矩陣和三角恆等式. II." Commun. Appl. Math. 3, 267-270, 1999.Cvijović, D. 和 Klinowski, J. "一些三角級數的封閉形式求和." Math. Comput. 64, 205-210, 1995.Edwards, H. M. 黎曼 zeta 函數. 紐約: Dover, 2001.Hansen, E. R. 級數和乘積表. Englewood Cliffs, NJ: Prentice-Hall, 1975.Olds, C. D. 連分數. 紐約: Random House, 1963.Project Mathematics. "正弦和餘弦，第一-三部分." 錄影帶. http://www.projectmathematics.com/sincos1.htm.Jeffrey, A. "三角恆等式." §2.4 見 數學公式和積分手冊，第 2 版. Orlando, FL: Academic Press, pp. 111-117, 2000.Spanier, J. 和 Oldham, K. B. "正弦 sin(x) 和餘弦 cos(x) 函數." 第 32 章 見 函數圖集. Washington, DC: Hemisphere, pp. 295-310, 1987.Tropfke, J. Teil IB, §1. "角的正弦和餘弦的概念." 見 基礎數學史系統表示法，特別考慮術語，第五卷，第二版. Berlin 和 Leipzig, Germany: de Gruyter, pp. 11-23, 1923.Trott, M. 符號運算的 Mathematica 指南. 紐約: Springer-Verlag, 2006. http://www.mathematicaguidebooks.org/.Zwillinger, D. (編). "三角函數或圓函數." §6.1 見 CRC 標準數學表格和公式. Boca Raton, FL: CRC Press, pp. 452-460, 1995.

在 中引用

正弦

引用為

Weisstein, Eric W. "正弦." 來自 Web 資源. https://mathworld.net.cn/Sine.html

主題分類