反双曲正弦  (Beyer 1987, p. 181; Zwillinger 1995, p. 481),有时称为面积双曲正弦(Harris 和 Stocker 1998, p. 264),是 多值函数,它是 反函数 双曲正弦。
(Beyer 1987, p. 181; Zwillinger 1995, p. 481),有时称为面积双曲正弦(Harris 和 Stocker 1998, p. 264),是 多值函数,它是 反函数 双曲正弦。
变体  或
或  (Harris 和 Stocker 1998, p. 263) 有时用于指代反双曲正弦的显式 主值,尽管这种区分并不总是明确的。更糟糕的是,符号
(Harris 和 Stocker 1998, p. 263) 有时用于指代反双曲正弦的显式 主值,尽管这种区分并不总是明确的。更糟糕的是,符号  有时用于主值,而
有时用于主值,而  用于多值函数 (Abramowitz 和 Stegun 1972, p. 87)。符号
用于多值函数 (Abramowitz 和 Stegun 1972, p. 87)。符号  (Jeffrey 2000, p. 124) 和
(Jeffrey 2000, p. 124) 和  (Gradshteyn 和 Ryzhik 2000, p. xxx) 有时也使用。请注意,在符号
(Gradshteyn 和 Ryzhik 2000, p. xxx) 有时也使用。请注意,在符号  中,
中, 是 双曲正弦,而上标
是 双曲正弦,而上标  表示 反函数,不是 乘法逆元。
表示 反函数,不是 乘法逆元。
它的 主值  在 Wolfram 语言 中实现为ArcSinh[z],在 GNU C 库中实现为asinh(double x)。
在 Wolfram 语言 中实现为ArcSinh[z],在 GNU C 库中实现为asinh(double x)。
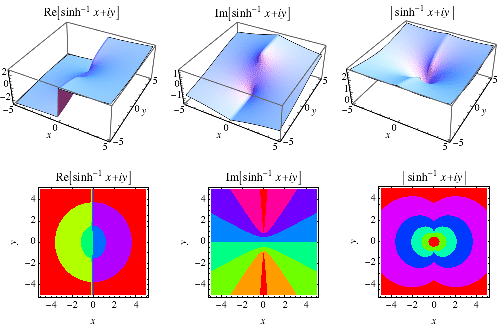
反双曲正弦是 多值函数,因此在 复平面 中需要 分支切割线,Wolfram 语言 的约定将其放置在线段  和
和  。这源于反双曲正弦的定义为
。这源于反双曲正弦的定义为
 |
(1)
|
反双曲正弦可以用 反函数 表示为
 |
(2)
|
(Gradshteyn 和 Ryzhik 2000, p. xxx)。
反双曲正弦的 导数 为
 |
(3)
|
且 不定积分 为
 |
(4)
|
它有麦克劳林级数
(OEIS A055786 和 A002595),其中  是 勒让德多项式。它在无穷远处有泰勒级数展开式
是 勒让德多项式。它在无穷远处有泰勒级数展开式
(OEIS A052468 和 A052469)。
另请参阅
双曲正弦,
反双曲函数
相关 Wolfram 站点
http://functions.wolfram.com/ElementaryFunctions/ArcSinh/
使用 探索
参考文献
Abramowitz, M. 和 Stegun, I. A. (Eds.). "Inverse Circular Functions." §4.4 in Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, 9th printing. New York: Dover, pp. 79-83, 1972.Beyer, W. H. CRC Standard Mathematical Tables, 28th ed. Boca Raton, FL: CRC Press, pp. 142-143, 1987.GNU C Library. "Mathematics: Inverse Trigonometric Functions." https://gnu.ac.cn/manual/glibc-2.2.3/html_chapter/libc_19.html#SEC391.Gradshteyn, I. S. 和 Ryzhik, I. M. Tables of Integrals, Series, and Products, 6th ed. San Diego, CA: Academic Press, p. xxx, 2000.Harris, J. W. 和 Stocker, H. Handbook of Mathematics and Computational Science. New York: Springer-Verlag, 1998.Jeffrey, A. "Inverse Trigonometric and Hyperbolic Functions." §2.7 in Handbook of Mathematical Formulas and Integrals, 2nd ed. Orlando, FL: Academic Press, pp. 124-128, 2000.Sloane, N. J. A. Sequences A002595/M4233, A052468, A052469, 和 A055786 in "The On-Line Encyclopedia of Integer Sequences."Spanier, J. 和 Oldham, K. B. "Inverse Trigonometric Functions." Ch. 35 in An Atlas of Functions. Washington, DC: Hemisphere, pp. 331-341, 1987.Zwillinger, D. (Ed.). "Inverse Hyperbolic Functions." §6.8 in CRC Standard Mathematical Tables and Formulae. Boca Raton, FL: CRC Press, pp. 481-483, 1995.在 中被引用
反双曲正弦
引用为
Weisstein, Eric W. "反双曲正弦。" 来自 Web 资源。 https://mathworld.net.cn/InverseHyperbolicSine.html
主题分类
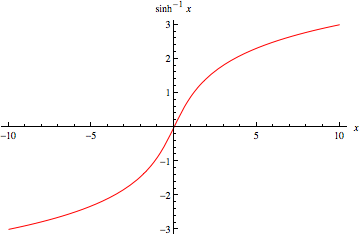
(Beyer 1987, p. 181; Zwillinger 1995, p. 481),有时称为面积双曲正弦(Harris 和 Stocker 1998, p. 264),是 多值函数,它是 反函数 双曲正弦。
或
(Harris 和 Stocker 1998, p. 263) 有时用于指代反双曲正弦的显式 主值,尽管这种区分并不总是明确的。更糟糕的是,符号
有时用于主值,而
用于多值函数 (Abramowitz 和 Stegun 1972, p. 87)。符号
(Jeffrey 2000, p. 124) 和
(Gradshteyn 和 Ryzhik 2000, p. xxx) 有时也使用。请注意,在符号
中,
是 双曲正弦,而上标
表示 反函数,不是 乘法逆元。
在 Wolfram 语言 中实现为ArcSinh[z],在 GNU C 库中实现为asinh(double x)。
和
。这源于反双曲正弦的定义为

是 勒让德多项式。它在无穷远处有泰勒级数展开式
