 |
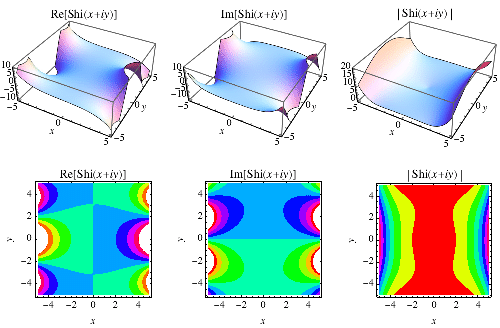 |
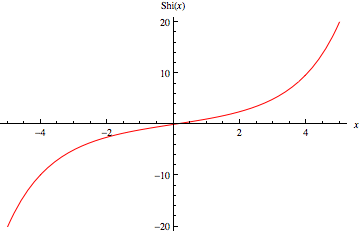
双曲正弦积分,通常简称 “Shi 函数”,定义为
|
(1)
|
该函数在 Wolfram 语言 中以函数形式实现SinhIntegral[z].
它具有麦克劳林级数
 |
(2)
| ||
|
(3)
|
(OEIS A061079)。
它具有导数
|
(4)
|
和不定积分
|
(5)
|
 |
 |
双曲正弦积分,通常简称 “Shi 函数”,定义为
|
(1)
|
该函数在 Wolfram 语言 中以函数形式实现SinhIntegral[z].
它具有麦克劳林级数
 |
(2)
| ||
|
(3)
|
(OEIS A061079)。
它具有导数
|
(4)
|
和不定积分
|
(5)
|
Weisstein, Eric W. “Shi。” 来自 Web 资源。 https://mathworld.net.cn/Shi.html