菜单图标 主题
Search

自然对数

下载 Mathematica 笔记本下载 Wolfram 笔记本
NaturalLogarithm

自然对数 lnx 是以 e 为底的 对数，其中

e=2.718281828....
(1)

此函数可以定义为

lnx=int_1^x(dt)/t
(2)

对于 x>0。

NaturalLogEPlot

此定义意味着 e 是唯一的数字，其性质是由 双曲线 y=1/x、x 轴以及垂直线 x=1 和 x=e 围成的区域面积为 1。换句话说，

int_1^e(dx)/x=lne=1.
(3)

符号 lnx 在物理学和工程学中用于表示自然对数，而数学家通常使用符号 logx。在本文中，lnx=log_ex 表示自然对数，而 logx=log_(10)x 表示常用对数。

关于自然对数幂的表示法有很多约定俗成的用法。虽然有些作者使用 ln^nz（即，使用类似于三角函数的约定），但通常也写作 (lnz)^n。

常用对数和自然对数可以互相表示为

lnx=(log_(10)x)/(log_(10)e)
(4)
log_(10)x=(lnx)/(ln10).
(5)

自然对数在微积分中尤其有用，因为它的导数由简单方程给出

d/(dx)lnx=1/x,
(6)

而其他底数的对数的导数则更复杂

d/(dx)log_bx=1/(xlnb).
(7)
NaturalLogBranchCut

自然对数可以解析延拓到复数，形式为

lnz=ln|z|+iarg(z),
(8)

其中 |z| 是复数模，arg(z) 是复数辐角。自然对数是多值函数，因此在复平面中需要分支切割线，Wolfram 语言的约定将其置于 (-infty,0]。

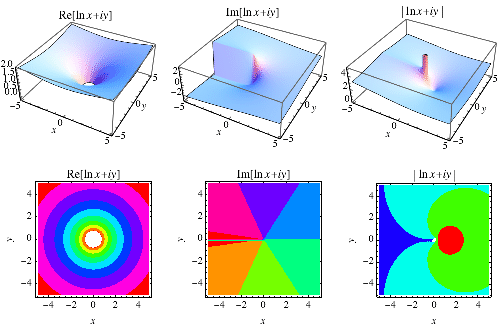NaturalLogReImAbs
最小值 最大值
实部
虚部 Powered by webMathematica

自然对数的主值在 Wolfram 语言中实现为Log[x]，等价于Log[E, x]。此函数在复平面中如上图所示。

请注意，反三角函数和反双曲函数可以用自然对数表示（实际上，通常定义为自然对数），如下表所示。因此，一旦这些定义达成一致，自然对数的分支切割线结构就确定了这些函数的分支切割线。

函数符号定义
反余割csc^(-1)z-iln(sqrt(1-1/(z^2)+i/z))
反余弦cos^(-1)z1/2pi+iln(iz+sqrt(1-z^2))
反余切cot^(-1)z1/2i[ln((z-i)/z)-ln((z+i)/z)]
反双曲余割csch^(-1)zln(sqrt(1+1/(z^2))+1/z)
反双曲余弦cosh^(-1)zln(z+sqrt(z-1)sqrt(z+1))
反双曲余切coth^(-1)z1/2[ln(1+1/z)-ln(1-1/z)]
反双曲正割sech^(-1)zln(sqrt(1/z-1)sqrt(1/z+1)+1/z)
反双曲正弦sinh^(-1)zln(z+sqrt(z^2+1))
反双曲正切tanh^(-1)z1/2[ln(1+z)-ln(1-z)]
反正割sec^(-1)z1/2pi+iln(sqrt(1-1/(z^2))+i/z)
反正弦sin^(-1)z-iln(iz+sqrt(1-z^2))
反正切tan^(-1)z1/2i[ln(1-iz)-ln(1+iz)]

墨卡托级数

ln(1+x)=x-1/2x^2+1/3x^3-...
(9)

给出了自然对数的泰勒级数。

对数函数的连分数表示包括

ln(1+x)=x/(1+(1^2x)/(2+(1^2x)/(3+(2^2x)/(4+(2^2x)/(5+(3^2x)/(6+(3^2x)/(7+...)))))))
(10)

（Lambert 1770; Lagrange 1776; Olds 1963, p. 138; Wall 1948, p. 342）和

ln((1+x)/(1-x))=(2x)/(1-(x^2)/(3-(4x^2)/(5-(9x^2)/(7-(16x^2)/(9-...)))))
(11)

（Euler 1813-1814; Wall 1948, p. 343; Olds 1963, p. 139）。

对于复数 z，自然对数满足

lnz=ln[re^(i(theta+2npi))]
(12)
=lnr+i(theta+2npi)
(13)

和

PV(lnz)=lnr+itheta,
(14)

其中 PV 是主值。

自然对数的一些特殊值包括

ln(-1)=ipi
(15)
ln0=-infty
(16)
ln1=0
(17)
lne=1
(18)
ln(+/-i)=+/-1/2pii.
(19)

自然对数有时可以写成“更简单”的对数的和或差，例如

ln(2+sqrt(3))=2ln(1+sqrt(3))-ln2,
(20)

这直接来自以下恒等式

2+sqrt(3)=1/2(1+sqrt(3))^2.
(21)

Plouffe (2006) 发现了以下优美的恒等式

ln2=10sum_(n=1)^(infty)1/(n(e^(pin)+1))+6sum_(n=1)^(infty)1/(n(e^(pin)-1))-4sum_(n=1)^(infty)1/(n(e^(2pin)-1))
(22)
ln3=9sum_(n=1)^(infty)1/(n(e^(pin)-1))+(49)/3sum_(n=1)^(infty)1/(n(e^(pin)+1))-(14)/3sum_(n=1)^(infty)1/(n(e^(2pin)+1))+sum_(n=1)^(infty)1/(n(e^(3pin)-1))-7/3sum_(n=1)^(infty)1/(n(e^(3pin)+1))+2/3sum_(n=1)^(infty)1/(n(e^(6pin)+1))
(23)
ln5=(57)/4sum_(n=1)^(infty)1/(n(e^(pin)-1))+(91)/4sum_(n=1)^(infty)1/(n(e^(pin)+1))-(13)/2sum_(n=1)^(infty)1/(n(e^(2pin)+1))+3/4sum_(n=1)^(infty)1/(n(e^(5pin)-1))-7/4sum_(n=1)^(infty)1/(n(e^(5pin)+1))+1/2sum_(n=1)^(infty)1/(n(e^(10pin)+1)).
(24)

另请参阅

常用对数, e, Lg, 对数, Nat, 自然对数焦散线, 2 的自然对数, 10 的自然对数 在 MathWorld 课堂中探索此主题

使用 Wolfram|Alpha 探索

参考文献

Euler, L. "Commentatio in fractionem continuam qua illustris La Grange potestates binomiales expressit." Mém. de l'Acad. imperiale des sciences de St. Pétersbourg 6, 1813-1814.Lagrange, J.-L. "Sur l'usage des fractions continues dans le calcul intégral." Nouv. mém. de l'académie royale des sciences et belles-lettres Berlin, 236-264, 1776. Reprinted in Oeuvres, Vol. 4, pp. 301-302.Lambert, J. L. Beiträge zum Gebrauch der Mathematik und deren Anwendung. Theil 2. Berlin, 1770.Olds, C. D. Continued Fractions. New York: Random House, 1963.Plouffe, S. "Identities Inspired from Ramanujan Notebooks (Part 2)." Apr. 2006. http://www.lacim.uqam.ca/~plouffe/inspired2.pdf.Wall, H. S. Analytic Theory of Continued Fractions. New York: Chelsea, 1948.Zwillinger, D. (Ed.). CRC Standard Mathematical Tables and Formulae, 30th ed. Boca Raton, FL: CRC Press, 1996.

在 Wolfram|Alpha 中被引用

自然对数

引用为

Weisstein, Eric W. "Natural Logarithm." 来自 MathWorld--Wolfram Web 资源。 https://mathworld.net.cn/NaturalLogarithm.html

主题分类