 |
(1)
|
其中 
是复数辐角。 明确地用实部和虚部表示，
![(a+bi)^(c+di)=(a^2+b^2)^(c/2)e^(-darg(a+ib))×{cos[carg(a+ib)+1/2dln(a^2+b^2)]+isin[carg(a+ib)+1/2dln(a^2+b^2)]}.](/images/equations/ComplexExponentiation/NumberedEquation2.svg) |
(2)
|
复数指数运算的一个明确例子由下式给出
![(1+i)^(1+i)=sqrt(2)e^(-pi/4)[cos(1/4pi+1/2ln2)+isin(1/4pi+1/2ln2)].](/images/equations/ComplexExponentiation/NumberedEquation3.svg) |
(3)
|
一个复数取复数幂可以是实数。 事实上，著名的例子
 |
(4)
|
表明纯虚数 
自乘幂是实数。
 |
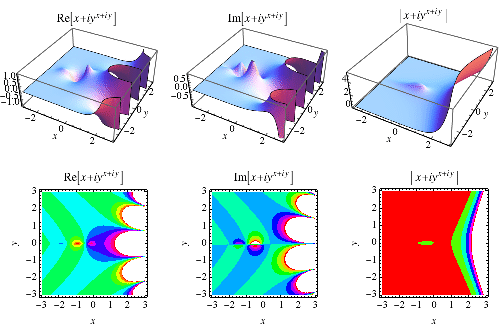事实上，存在一系列值 
使得 
是实数，正如通过以下表达式可以看出
![(ik)^(ik)=e^(-kpi/2)[cos(klnk)+isin(klnk)].](/images/equations/ComplexExponentiation/NumberedEquation5.svg) |
(5)
|
当 
时，这将是实数，即，对于
 |
(6)
|
对于 
整数。 对于正 
，这给出根 
或者
 |
(7)
|
其中 
是 Lambert W 函数。 对于 
，这简化为
 |
(8)
|
对于 
, 2, ..., 这些给出数值 1, 2.92606 (OEIS A088928), 4.30453, 5.51798, 6.63865, 7.6969, ....
