立方根

最小值 最大值

最小值 最大值 实部 虚部

给定一个数 ， 的立方根，记作 或 ( 的 1/3 次方)，是一个数 ，使得 。因此，立方根是 n 次根，其中 。每个实数都有唯一的实立方根，并且每个非零复数都有三个不同的立方根。

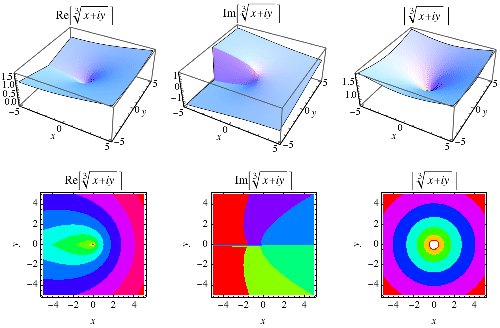
负数的立方根的教科书定义是 。然而，将立方根扩展到复平面会沿着负实轴产生分支切割，如上图所示，这是立方根的主值。按照惯例，“the”（主要的）立方根因此是一个具有正虚部的复数。因此，Wolfram 语言和其他符号代数语言和程序返回在整个复平面上有效的结果，因此对于 返回复数结果。例如，在 Wolfram 语言中，ComplexExpand[(-1)^(1/3)] 给出结果 。

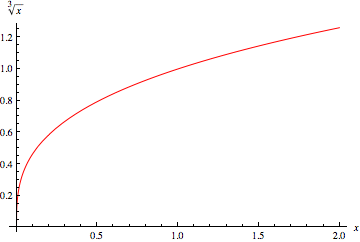
当考虑正实数 时，Wolfram 语言函数CubeRoot[x]，它等价于Surd[x, 3]，可以用来返回实立方根。

数字 的立方根可以使用牛顿法计算，通过迭代应用

对于一些实数起始值 。