平方根

最小值 最大值

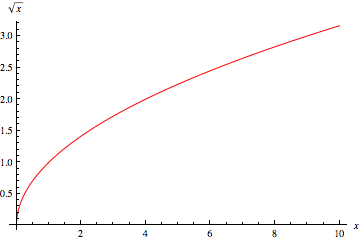
一个数 的平方根是一个数 ，使得 。当写成 的形式，或者特别是 时， 的平方根也可以称为根式或根式。因此，平方根是 n次根，其中 。

请注意，任何正实数都有两个平方根，一个正数和一个负数。例如，9 的平方根是 和 ，因为 。任何非负实数 都有唯一的非负平方根 ；这被称为主平方根，并写作 或 。例如，9 的主平方根是 ，而 9 的另一个平方根是 。在通常用法中，除非另有说明，“平方根”通常指主平方根。主平方根函数 是 在 时的反函数。

最小值 最大值 实部 虚部

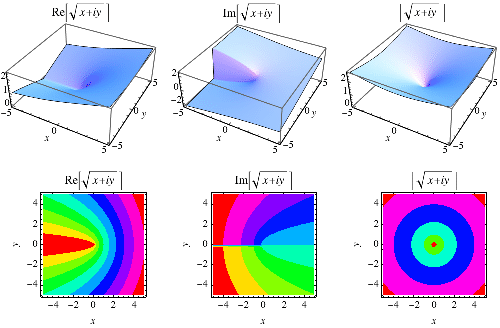任何非零复数 也都有两个平方根。例如，使用虚数单位 i， 的两个平方根是 。数字 的主平方根表示为 (如同正实数情况)，并由 Wolfram 语言函数返回Sqrt[z].

当考虑正实数 时，可以使用 Wolfram 语言函数Surd[x, 2] 来返回实平方根。

复数 的平方根由下式给出

(1)

此外，

(2)

正如在上图中可以看到的，复数平方根函数的虚部沿着负实轴有一个分支切割线。

有许多平方根算法可以用来逼近给定（正实数）数字的平方根。这些算法包括 Bhaskara-Brouncker 算法和 Wolfram 迭代。最简单的 算法是牛顿迭代法

(3)

其中 。

2 的平方根是无理数 (OEIS A002193)，有时被称为毕达哥拉斯常数，它具有简单的周期连分数 [1, 2, 2, 2, 2, 2, ...] (OEIS A040000)。3 的平方根是无理数 (OEIS A002194)，有时被称为狄奥多罗斯常数，它具有简单的周期连分数 [1, 1, 2, 1, 2, 1, 2, ...] (OEIS A040001)。一般来说，所有正整数的平方根的连分数都是周期性的。

形如 的嵌套根式有时可以通过等式简化为简单的平方根

(4)

平方得到

(5)

因此

			(6)
			(7)

求解 和 得到

(8)

例如，

(9)

(10)

SimplifyWolfram 语言的 Simplify 命令不应用此类简化，但是FullSimplify会应用此类简化。一般来说，根式去嵌套是一个难题 (Landau 1992ab, 1994, 1998)。

反函数的反直觉性质是

(11)

因此，预期的恒等式（即， 的抵消）不沿着负实轴成立。