外接圆心三角形

三角形 的外接圆心三角形，也称为三切线三角形，是顶点对应于 旁心 的 三角形 。

它是关于 内心 的反切维安三角形 (Kimberling 1998, p. 157)，也是关于 的反垂足三角形。

外接圆心三角形的外接圆是 Bevan 圆。

它的三线顶点矩阵是

(1)

外接圆心三角形的边长为

			(2)
			(3)
			(4)

面积为

			(5)
			(6)

其中 、 和 分别是原始三角形 的面积、内切圆半径和半周长。因此，它与六线三角形具有相同的边长和面积。

外接圆心三角形透视于每个塞维安三角形 (Kimberling 1998, p. 157)。

外接圆心-六线椭圆穿过外接圆心三角形和六线三角形的顶点。

从任意三角形 开始，找到外接圆心三角形 。然后找到该三角形的外接圆心三角形 ，依此类推。那么，得到的三角形 趋近于等边三角形 (Johnson 1929, p. 185; Goldoni 2003)。对于接触三角形的迭代构造，也存在类似的结果 (Goldoni 2003)。

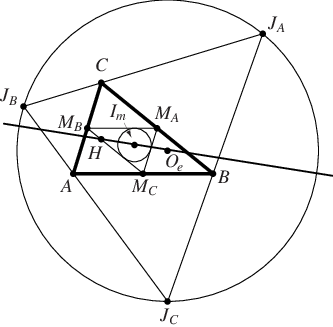
给定一个三角形 ，绘制外接圆心三角形 和中点三角形 。那么 的垂心 、 的内心 和 的外心 与 （ 的中点）共线 (Honsberger 1995)。

的内心 与 的垂心 重合，并且 的外心 与 的九点圆圆心 重合。此外， 是连接 的垂心 和 外心 的线段的中点 (Honsberger 1995)。

下表给出了外接圆心三角形的中心，以参考三角形的中心表示，对于 Kimberling 中心 ，其中 。

	外接圆心三角形的中心		参考三角形的中心
	内心		外接圆心三角形的内心
	三角形质心		外接圆心三角形的三角形质心
	外心		Bevan 点
	垂心		内心
	九点圆圆心		外心
	外心对称点		Mittenpunkt
	Gergonne 点		外接圆心三角形的 Gergonne 点
	Nagel 点		外接圆心三角形的 Nagel 点
	Mittenpunkt		外接圆心三角形的 Mittenpunkt
	第一等力点		第三 Evans 透视点
	第二等力点		第二 Evans 透视点
	Clawson 点		全等等腰化线点
	abc 和垂足三角形的垂足三角形的透视点		-Ceva 共轭于
	垂足三角形和切线三角形的位似中心		等角共轭于
	欧拉无穷远点		等角共轭于
	第二幂点		全等外接圆等腰化线点
	第三幂点		-Ceva 共轭于
	垂足三角形和内切三角形的透视点		全等内切圆等腰化线点
	-Ceva 共轭于		第三等腰化线点
	和 的交点		第二等腰化线点
	垂足三角形的三角形质心		三角形质心
	垂足三角形的垂心		垂心
	垂足三角形的外心对称点		外心对称点
	Kosnita 点		-Ceva 共轭于
	等角共轭于		等周长等腰化线点
	等角共轭于		直线 和 的交点
	等角共轭于		的本征变换
	接触三角形的垂心		反补三角形的第二中弧点
	Prasolov 点		直线 和 的交点
	反补三角形的外心对称点		外接圆心等角共轭于
	内心的等张共轭		直线 和 的交点
	第三 Brocard 点		-aleph 共轭于
	内心和 Clawson 点的 Cevapoint		第一等腰化线点
	三角形质心和外心的 Cevapoint		外接圆心等角共轭于
	等角共轭于		外接圆心等角共轭于
	等角共轭于		外接圆心等角共轭于
	Tarry 点		第五 Sharygin 点