连接位似图形的对应点的直线的交点。在上图中, 是位似图形
和
的位似中心。对于相似但不具有平行边的图形,存在相似中心(Johnson 1929,第 16-20 页)。
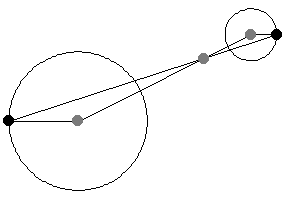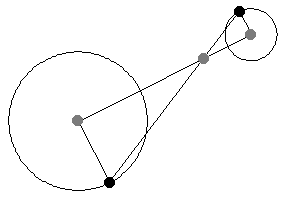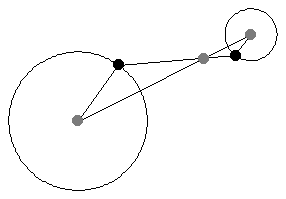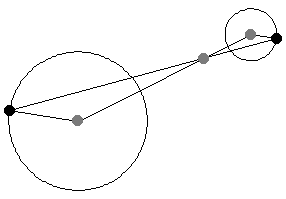
给定两个非同心圆,绘制半径,使其平行且方向相同。然后,连接半径端点的直线穿过中心连线上的一定点,该点将中心连线按半径之比外分。此点称为外位似中心,或外相似中心(Johnson 1929,第 19-20 和 41 页)。
如果半径被绘制为平行,但方向相反,则半径的端点穿过中心连线上的一定点,该点将中心连线按半径之比内分(Johnson 1929,第 19-20 和 41 页)。此点称为内位似中心,或内相似中心(Johnson 1929,第 19-20 和 41 页)。
对于半径为 、中心为
以及线段角度为
的两个圆,位似中心的位置通过解以下联立方程组给出
|
(1)
| |||
|
(2)
|
求解 ,其中
|
(3)
| |||
|
(4)
|
加号给出外位似中心,而减号给出内位似中心。
|
|
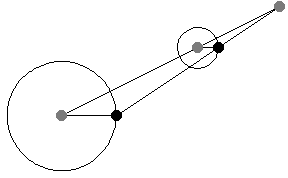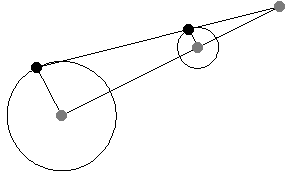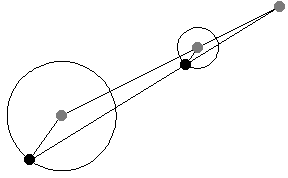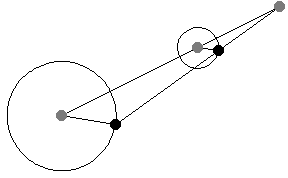
如上图所示,当平行线段的角度变化时,位似中心的位置保持不变。这一事实为将一个半径的圆周运动转换为另一个半径的圆周运动提供了一种(开槽)连杆机构。
三个圆的六个位似中心,每三个共线,共四条线(Johnson 1929,第 120 页),这些线“包围”着最小的圆。