双阶乘 -- 来自 Wolfram MathWorld

双阶乘

正整数的双阶乘是通常阶乘 $n!\$ 的推广，定义为

n!!={n·(n-2)...5·3·1 n>0 odd; n·(n-2)...6·4·2 n>0 even; 1 n=-1,0.

(1)

注意，，根据定义 (Arfken 1985, p. 547)。

符号的起源似乎不广为人知，并且在 Cajori (1993) 中没有提及。

对于 , 1, 2, ...，前几个值是 1, 1, 2, 3, 8, 15, 48, 105, 384, ... (OEIS A006882)。的十进制位数，对于 , 1, ... 是 1, 4, 80, 1285, 17831, 228289, 2782857, 32828532, ... (OEIS A114488)。

双阶乘在 Wolfram 语言中以 n!! 或Factorial2[n]。

双阶乘是多阶乘的一个特例。

双阶乘可以用伽玛函数表示为

(2)

(Arfken 1985, p. 548)。

双阶乘也可以使用定义扩展到负奇整数

			(3)
			(4)

对于 , 1, ... (Arfken 1985, p. 547)。

	最小值	最大值
实部
虚部

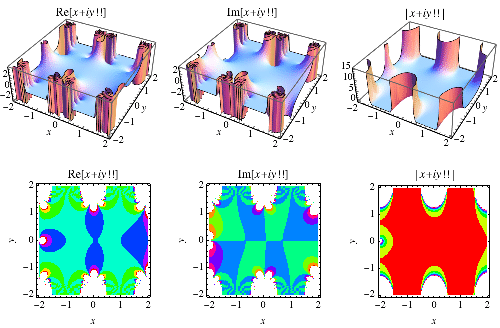类似地，双阶乘可以扩展到复数参数，表示为

(5)

有很多恒等式将双阶乘与阶乘联系起来。由于

(2n+1)!!2^nn!
=[(2n+1)(2n-1)...1][2n][2(n-1)][2(n-2)]...2·1
=[(2n+1)(2n-1)...1][2n(2n-2)(2n-4)...2]
=(2n+1)(2n)(2n-1)(2n-2)(2n-3)(2n-4)...2·1
=(2n+1)!,

(6)

由此得出。对于 , 1, ...，前几个值是 1, 3, 15, 105, 945, 10395, ... (OEIS A001147)。

同样，由于

			(7)
			(8)
			(9)

由此得出 $(2n)!!=2^nn!\$ 。对于 , 1, ...，前几个值是 1, 2, 8, 48, 384, 3840, 46080, ... (OEIS A000165)。

最后，由于

(2n-1)!!2^nn!
=[(2n-1)(2n-3)...1][2n][2(n-1)][2(n-2)]...2(1)
=(2n-1)(2n-3)...1][2n(2n-2)(2n-4)...2]
=2n(2n-1)(2n-2)(2n-3)(2n-4)...2(1)
=(2n)!,

(10)

由此得出

(11)

对于 $n\$ 奇数，

			(12)
			(13)
			(14)

对于 $n\$ 偶数，

			(15)
			(16)
			(17)

因此，对于任何 $n\$ ，

(18)

(19)

双阶乘满足以下漂亮的级数

			(20)
			(21)
			(22)

后者给出了倒数双阶乘的闭合形式的和，如下所示

			(23)
			(24)
			(25)

(OEIS A143280)，其中是一个下不完全伽玛函数。这个和是倒数多阶乘常数的一个特例。

拉马努金给出的一个闭合形式的和由下式给出

(26)

(Hardy 1999, p. 106)。Whipple (1926) 给出了这个和的推广 (Hardy 1999, pp. 111-112)。

参考文献

Arfken, G. Mathematical Methods for Physicists, 3rd ed. Orlando, FL: Academic Press, pp. 544-545 and 547-548, 1985.

Meserve, B. E. "Double Factorials." Amer. Math. Monthly 55, 425-426, 1948.

Sloane, N. J. A. Sequences A000165/M1878, A001147/M3002, A006882/M0876, A114488, and A143280 in "The On-Line Encyclopedia of Integer Sequences."

Whipple, F. J. W. "On Well-Poised Series, Generalised Hypergeometric Series Having Parameters in Pairs, Each Pair with the Same Sum." Proc. London Math. Soc. 24, 247-263, 1926.

双阶乘

另请参阅

相关 Wolfram 网站

使用 Wolfram|Alpha 探索

参考文献

在 Wolfram|Alpha 中被引用

请引用为

主题分类