双伽玛函数是一个特殊函数,它由伽玛函数的对数导数(或,取决于定义,阶乘的对数导数)给出。
由于这种歧义,有时(但并非总是)使用两种不同的符号,其中
 |
(1)
|
定义为伽玛函数  的对数导数,并且
的对数导数,并且
 |
(2)
|
定义为阶乘函数的对数导数。两者通过以下关系连接:
 |
(3)
|
 阶导数
阶导数  被称为多伽玛函数,表示为
被称为多伽玛函数,表示为  。因此,符号
。因此,符号
 |
(4)
|
经常用于双伽玛函数本身,Erdélyi et al. (1981) 使用符号  表示
表示  。双伽玛函数
。双伽玛函数  由函数返回PolyGamma[z] 或PolyGamma[0, z] 在 Wolfram 语言中,并使用符号
由函数返回PolyGamma[z] 或PolyGamma[0, z] 在 Wolfram 语言中,并使用符号  排版。
排版。
双伽玛函数出现在简单的求和中,例如
其中  是一个 Lerch 超越函数。
是一个 Lerch 超越函数。
特殊情况如下:
高斯双伽玛定理指出
![(Gamma^'(p/q))/(Gamma(p/q))=-gamma-ln(2q)-1/2picot((pip)/q)+2sum_(0<n<q/2)cos((2pipn)/q)ln[sin((pin)/q)]](/images/equations/DigammaFunction/NumberedEquation5.svg) |
(11)
|
(Allouche 1992,Knuth 1997,第 94 页)。
双伽玛函数的渐近级数由下式给出
其中  是欧拉-马歇罗尼常数,
是欧拉-马歇罗尼常数, 是伯努利数。
是伯努利数。
双伽玛函数满足
 |
(17)
|
对于整数  ,
,
 |
(18)
|
其中  是欧拉-马歇罗尼常数,
是欧拉-马歇罗尼常数, 是调和数。
是调和数。
其他恒等式包括
 |
(19)
|
 |
(20)
|
 |
(21)
|
 |
(22)
|
特殊值是
在整数值处,
(Derbyshire 2004,第 58 页),在半整数值处,
其中  是调和数。
是调和数。
它由单位正方形积分给出
 |
(29)
|
对于  (Guillera 和 Sondow 2005)。代入
(Guillera 和 Sondow 2005)。代入  给出了一个涉及欧拉-马歇罗尼常数的特殊情况。
给出了一个涉及欧拉-马歇罗尼常数的特殊情况。
 的级数由下式给出
的级数由下式给出
 |
(30)
|
对数级数由下式给出
 |
(31)
|
(Guillera 和 Sondow 2005)。
从FoxTrot 级数中出现的一个令人惊讶的恒等式由下式给出
 |
(32)
|
另请参阅
Barnes G-函数,
G-函数,
伽玛函数,
高斯双伽玛定理,
调和数,
Hurwitz Zeta 函数,
对数导数,
梅林公式,
多伽玛函数,
拉马努金 phi-函数,
三伽玛函数
Wolfram 相关站点
http://functions.wolfram.com/GammaBetaErf/PolyGamma/
使用 探索
参考文献
Abramowitz, M. 和 Stegun, I. A. (Eds.). "Psi (Digamma) Function." §6.3 in Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, 9th printing. New York: Dover, pp. 258-259, 1972.Allouche, J.-P. "Series and Infinite Products related to Binary Expansions of Integers." 1992. http://algo.inria.fr/seminars/sem92-93/allouche.ps.Arfken, G. "Digamma and Polygamma Functions." §10.2 in Mathematical Methods for Physicists, 3rd ed. Orlando, FL: Academic Press, pp. 549-555, 1985.Boros, G. 和 Moll, V. "The Psi Function." §10.11 in Irresistible Integrals: Symbolics, Analysis and Experiments in the Evaluation of Integrals. Cambridge, England: Cambridge University Press, pp. 212-215, 2004.Derbyshire, J. Prime Obsession: Bernhard Riemann and the Greatest Unsolved Problem in Mathematics. New York: Penguin, 2004.Erdélyi, A.; Magnus, W.; Oberhettinger, F.; 和 Tricomi, F. G. "The  Function." §1.7 in Higher Transcendental Functions, Vol. 1. New York: Krieger, pp. 15-20, 1981.Guillera, J. 和 Sondow, J. "Double Integrals and Infinite Products for Some Classical Constants Via Analytic Continuations of Lerch's Transcendent." 16 June 2005 http://arxiv.org/abs/math.NT/0506319.Havil, J. Gamma: Exploring Euler's Constant. Princeton, NJ: Princeton University Press, 2003.Jeffreys, H. 和 Jeffreys, B. S. "The Digamma (
Function." §1.7 in Higher Transcendental Functions, Vol. 1. New York: Krieger, pp. 15-20, 1981.Guillera, J. 和 Sondow, J. "Double Integrals and Infinite Products for Some Classical Constants Via Analytic Continuations of Lerch's Transcendent." 16 June 2005 http://arxiv.org/abs/math.NT/0506319.Havil, J. Gamma: Exploring Euler's Constant. Princeton, NJ: Princeton University Press, 2003.Jeffreys, H. 和 Jeffreys, B. S. "The Digamma ( ) and Trigamma (
) and Trigamma ( ) Functions." Methods of Mathematical Physics, 3rd ed. Cambridge, England: Cambridge University Press, pp. 465-466, 1988.Knuth, D. E. The Art of Computer Programming, Vol. 1: Fundamental Algorithms, 3rd ed. Reading, MA: Addison-Wesley, 1997.Spanier, J. 和 Oldham, K. B. "The Digamma Function
) Functions." Methods of Mathematical Physics, 3rd ed. Cambridge, England: Cambridge University Press, pp. 465-466, 1988.Knuth, D. E. The Art of Computer Programming, Vol. 1: Fundamental Algorithms, 3rd ed. Reading, MA: Addison-Wesley, 1997.Spanier, J. 和 Oldham, K. B. "The Digamma Function  ." Ch. 44 in An Atlas of Functions. Washington, DC: Hemisphere, pp. 423-434, 1987.
." Ch. 44 in An Atlas of Functions. Washington, DC: Hemisphere, pp. 423-434, 1987.在 中被引用
双伽玛函数
请引用为
Weisstein, Eric W. "双伽玛函数。" 来自 --一个 资源。 https://mathworld.net.cn/DigammaFunction.html
主题分类
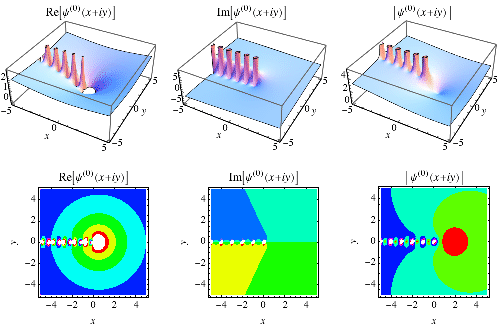
表示
。双伽玛函数
由函数返回PolyGamma[z] 或PolyGamma[0, z] 在 Wolfram 语言中,并使用符号
排版。

是一个 Lerch 超越函数。





![(Gamma^'(p/q))/(Gamma(p/q))=-gamma-ln(2q)-1/2picot((pip)/q)+2sum_(0<n<q/2)cos((2pipn)/q)ln[sin((pin)/q)]](/images/equations/DigammaFunction/NumberedEquation5.svg)
,



是调和数。
(Guillera 和 Sondow 2005)。代入
给出了一个涉及欧拉-马歇罗尼常数的特殊情况。
的级数由下式给出
