余割
其中 正弦 。余割在 Wolfram 语言 中被实现为Csc z ].
符号 et al. 1989, p. 222; Gradshteyn and Ryzhik 2000, p. xxix)。注意到余割在欧洲似乎没有得到一致的广泛使用，尽管它在各种德国和俄罗斯手册中明确出现（例如，Gellert et al. 1989, p. 222; Gradshteyn and Ryzhik 2000, pp. xxix 和 p. 43）。有趣的是，虽然 et al. 1989, p. 222），但在另一些表格中却没有（Gradshteyn and Ryzhik 2000，他们在第 28 页的“基本函数关系”表中没有列出它，但在第 43 页给出了涉及它的恒等式）。
Harris 和 Stocker (1998, p. 300) 称正割和余割为“极少使用的函数”，但随后用一整节来介绍它们。由于这些函数在美国似乎确实被广泛使用（例如，Abramowitz 和 Stegun 1972, p. 72），关于它们消亡的报道似乎有点为时过早。
导数是
(3)
不定积分是
(4)
其中 积分常数 。对于实轴上的
余割函数的洛朗级数是
(OEIS A036280 和 A036281 )，其中 伯努利数 。
给出 A046947 )，这些值恰好是
另请参阅 Flint Hills 级数 ,
反余割 ,
正割 ,
正弦
相关的 Wolfram 网站 http://functions.wolfram.com/ElementaryFunctions/Csc/
使用 Wolfram|Alpha 探索
参考文献 Abramowitz, M. and Stegun, I. A. (Eds.). "Circular Functions." §4.3 in Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, 9th printing. Beyer, W. H. CRC Standard Mathematical Tables, 28th ed. Gellert, W.; Gottwald, S.; Hellwich, M.; Kästner, H.; and Künstner, H. (Eds.). VNR Concise Encyclopedia of Mathematics, 2nd ed. Gradshteyn, I. S. and Ryzhik, I. M. Tables of Integrals, Series, and Products, 6th ed. Harris, J. W. and Stocker, H. "Secant and Cosecant." §5.34 in Handbook of Mathematics and Computational Science. Jeffrey, A. "Trigonometric Identities." §2.4 in Handbook of Mathematical Formulas and Integrals, 2nd ed. Sloane, N. J. A. Sequences A036280 , A036281 , and A046947 in "The On-Line Encyclopedia of Integer Sequences." Spanier, J. and Oldham, K. B. "The Secant An Atlas of Functions. Tropfke, J. Teil IB, §3. "Die Begriffe von Sekans und Kosekans eines Winkels." In Geschichte der Elementar-Mathematik in systematischer Darstellung mit besonderer Berücksichtigung der Fachwörter, fünfter Band, zweite aufl. Berlin and Leipzig, Germany: de Gruyter, pp. 28-30, 1923. Zwillinger, D. (Ed.). "Trigonometric or Circular Functions." §6.1 in CRC Standard Mathematical Tables and Formulae. 在 Wolfram|Alpha 中被引用 余割
请这样引用
Weisstein, Eric W. "余割。" 来自 MathWorld https://mathworld.net.cn/Cosecant.html
学科分类
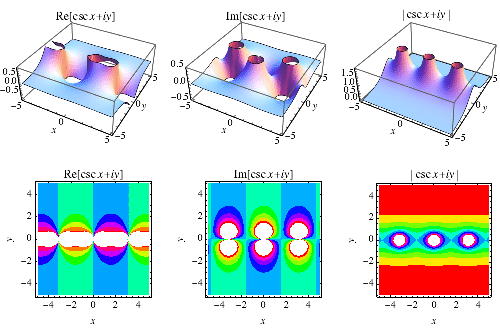
是由以下定义的函数
是 正弦。余割在 Wolfram 语言中被实现为Csc[z].
有时也被使用 (Gellert et al. 1989, p. 222; Gradshteyn and Ryzhik 2000, p. xxix)。注意到余割在欧洲似乎没有得到一致的广泛使用，尽管它在各种德国和俄罗斯手册中明确出现（例如，Gellert et al. 1989, p. 222; Gradshteyn and Ryzhik 2000, pp. xxix 和 p. 43）。有趣的是，虽然 
在一些表格中与其他三角函数同等对待（Gellert et al. 1989, p. 222），但在另一些表格中却没有（Gradshteyn and Ryzhik 2000，他们在第 28 页的“基本函数关系”表中没有列出它，但在第 43 页给出了涉及它的恒等式）。
![intcsczdz=ln[sin(1/2z)]-ln[cos(1/2z)]+C,](/images/equations/Cosecant/NumberedEquation2.svg)
是积分常数。对于实轴上的 
，这简化为
![ln[tan(1/2z)]+C](/images/equations/Cosecant/Inline15.svg)
是伯努利数。
递增最大值的 
的正整数值由 1, 3, 22, 333, 355, 103993, ... 给出 (OEIS A046947)，这些值恰好是 
的收敛项的分子，并对应于值 1.1884, 7.08617, 112.978, 113.364, 33173.7, ....
and Cosecant 
Functions." Ch. 33 in