主题
Search

Sinc 函数

下载 Mathematica Notebook下载 Wolfram Notebook
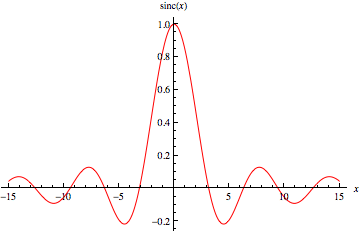
SincReal
最小值 最大值
Powered by webMathematica

sinc 函数 sinc(x)，也称为“采样函数”，是在信号处理和 傅里叶变换 理论中经常出现的一个函数。该函数的全称是“sine cardinal”，但通常以其缩写“sinc”来称呼。通常使用两种定义。本文采用的定义是

sinc(x)={1 for x=0; (sinx)/x otherwise,
(1)

其中 sinx 是 正弦 函数，如上图所示。

这具有归一化

int_(-infty)^inftysinc(x)dx=pi.
(2)

此函数在 Wolfram 语言 中实现为Sinc[x]。

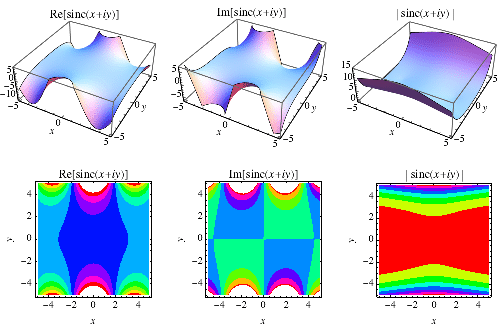SincReImAbs
最小值 最大值
Re
Im Powered by webMathematica

当扩展到 复平面 时，sinc(z) 如上图所示。

SincCos

关于 sinc(x) 的一个有趣的性质是，sinc(x) 的 局部极值 集合对应于其与 余弦 函数 cos(x) 的交点，如上图所示。

导数 由下式给出

(dsinc(z))/(dz)=(cosz)/z-(sinz)/(z^2)
(3)

不定积分 由下式给出

intsinc(z)dz=Si(z),
(4)

其中 Si(z) 是 正弦积分。

Woodward (1953)、McNamee et al. (1971) 和 Bracewell (1999, p. 62) 采用了另一种定义

sinc_pi(x)=sinc(pix)
(5)
={1 for x=0; (sin(pix))/(pix) otherwise.
(6)

后一种定义有时更方便，因为它具有简单的归一化，

int_(-infty)^inftysinc_pi(x)dx=1.
(7)

该变体也满足求和式

sum_(k=-infty)^inftysinc(pik)=1.
(8)

此外，二项式系数 满足

(0; x)=sinc_(pi)(x),
(9)

这本质上是 反射关系 的重述

Gamma(1+x)Gamma(1-x)=(pix)/(sin(pix))=1/(sinc_(pi)(x))
(10)

伽玛函数 的反射关系 (M. Somos, 私人通讯，2006 年 10 月 26 日)。

sinc 函数与 第一类球贝塞尔函数 j_n(x) 密切相关，特别是

sinc(x)=j_0(x),
(11)

并且用 Meijer G-函数 表示为

sinc(z)=(sqrt(pi))/2G_(02)^(10)(1/2z,1/2|-; 0,1/2).
(12)

设 Pi(x) 为 矩形函数，则 Pi(x) 的 傅里叶变换 是 sinc 函数

F_x[Pi(x)](k)=sinc(pik).
(13)

因此，sinc 函数经常出现在物理应用中，例如傅里叶变换光谱学中，作为所谓的 仪器函数，它给出了仪器对 delta 函数 输入的响应。从最终光谱中去除仪器函数需要使用某种 反卷积 算法。

sinc 函数可以写成复数 积分，注意到，对于 x!=0,

sinc(nx)=(sin(nx))/(nx)
(14)
=1/(nx)(e^(inx)-e^(-inx))/(2i)
(15)
=1/(2inx)[e^(itx)]_(-n)^n
(16)
=1/(2n)int_(-n)^ne^(ixt)dt,
(17)

并且对于 x=0，sinc(nx) 和积分都等于 1。

sinc 函数也可以写成 无穷乘积

sinc(x)=product_(k=1)^inftycos(x/(2^k)),
(18)

这是 François Viète 在 1593 年发现的结果 (Kac 1959, Morrison 1995)，有时被称为欧拉公式 (Prudnikov et al. 1986, p. 757; Gearhart and Shulz 1990)。它也由下式给出

sinc(x)=product_(k=1)^infty(1-(x^2)/(k^2pi^2))
(19)

(Gearhart and Shulz 1990) 和

sinc(x)=product_(k=1)^infty[1-4/3sin^2(x/(3^k))]
(20)

(Prudnikov et al. 1986, p. 757)。

另一个乘积由下式给出

product_(k=1)^(infty)sinc((2pi)/(2k+1))=pi/(2K)
(21)
=0.1805504...
(22)

(OEIS A118253; Prudnikov et al. 1986, p. 757)，其中 K=8.700... 是来自 多边形外切 的常数。

正整数上的 sinc(k) 幂的和包括

sum_(k=1)^(infty)sinc(k)=-1/2+1/2pi
(23)
sum_(k=1)^(infty)sinc^2(k)=-1/2+1/2pi
(24)
sum_(k=1)^(infty)sinc^3(k)=-1/2+3/8pi
(25)
sum_(k=1)^(infty)sinc^4(k)=-1/2+1/3pi
(26)
sum_(k=1)^(infty)sinc^5(k)=-1/2+(115)/(384)pi
(27)
sum_(k=1)^(infty)sinc^6(k)=-1/2+(11)/(40)pi.
(28)

sinc(k) 和 sinc(k)^2 的和相等这个惊人的事实似乎最早发表在 Baillie (1978) 中。令人惊讶的是，这些和等于 -1/2 加上 pi 的有理倍数的模式在幂 n=7 时被打破，此时和等于

sum_(k=1)^inftysinc^7(k)=-1/2+P(x),
(29)

其中

P(x)=1/(46080)pi(129423-201684pi+144060pi^2-54880pi^3+11760pi^4-1344pi^5+64pi^6).
(30)

sinc 函数满足恒等式

int_(-infty)^inftysinc[pi(x-y)]sinc(piy)dy=sinc(pix).
(31)

涉及 sinc 函数的定积分包括

int_0^inftysinc(x)dx=1/2pi
(32)
int_0^inftysinc^2(x)dx=1/2pi
(33)
int_0^inftysinc^3(x)dx=3/8pi
(34)
int_0^inftysinc^4(x)dx=1/3pi
(35)
int_0^inftysinc^5(x)dx=(115)/(384)pi.
(36)

在除以常数因子 pi 后，这些值再次为 1/2、1/2、3/8、1/3、115/384、11/40、5887/23040、151/630、259723/1146880、... (OEIS A049330 和 A049331; Grimsey 1945, Medhurst and Roberts 1965)。这些都是惊人的通用结果的特例

int_0^infty(sin^ax)/(x^b)dx=(pi^(1-c)(-1)^(|_(a-b)/2_|))/(2^(a-c)(b-1)!)sum_(k=0)^(|_a/2_|-c)(-1)^k(a; k)(a-2k)^(b-1)[ln(a-2k)]^c,
(37)

其中 a 和 b 是 正整数，使得 a>=b>c，c=a-b (mod 2)，|_x_| 是 向下取整函数，并且 0^0 被视为等于 1 (Kogan; 参见 Espinosa 和 Moll 2000)。当 n 是 正 偶数 整数时，这个壮观的公式简化为特殊情况

int_0^infty(sin^(2n)x)/(x^(2n))dx=pi/(2(2n-1)!)<2n-1; n-1>,
(38)

其中 <n; k> 是 欧拉数 (Kogan; 参见 Espinosa 和 Moll 2000)。积分的解也可以用系数的 递推关系 来表示

c(a,b)={pi/(2^(a+1-b))(a-1; 1/2(a-1)) for b=1 or b=2; (a[(a-1)c(a-2,b-2)-a·c(a,b-2)])/((b-1)(b-2)) otherwise.
(39)
SincContour

可以使用 轮廓积分 推导出 sinc(x) 的半无穷积分。在上图中，考虑路径 gamma=gamma_1+gamma_(12)+gamma_2+gamma_(21)。现在写 z=Re^(itheta)。在弧线上，dz=iRe^(itheta)dtheta，在 x 轴 上，dz=e^(itheta)dR。写

int_(-infty)^inftysinc(x)dx=Iint_gamma(e^(iz))/zdz,
(40)

其中 I 表示 虚部。现在定义

I=int_(-infty)^infty(e^(iz))/zdz
(41)
=lim_(R_1->0)int_pi^0(exp(iR_1e^(itheta)))/(R_1e^(itheta))iR_1e^(itheta)dtheta+lim_(R_1->0)lim_(R_2->infty)int_(R_1)^(R_2)(e^(iR))/RdR+lim_(R_2->infty)int_0^pi(exp(iz))/zdz+lim_(R_1->0; R_2->infty)int_(R_2)^(R_1)(e^(-iR))/(-R)(-dR),
(42)

其中第二项和第四项使用了恒等式 e^(i0)=1 和 e^(ipi)=-1。简化后，

I=lim_(R_1->0)int_pi^0exp(iR_1e^(itheta))idtheta+int_(0^+)^infty(e^(iR))/RdR+lim_(R_2->infty)int_0^pi(exp(iz))/zdz+int_infty^(0^+)(e^(-iR))/(-R)(-dR)
(43)
=-int_0^piidtheta+int_(0^+)^infty(e^(iR))/RdR+0+int_(-infty)^(0^-)(e^(iR))/RdR,
(44)

其中第三项通过 约尔当引理 消失。对第一项进行积分并组合其他项得到

I=-ipi+int_(-infty)^infty(e^(iz))/zdz=0.
(45)

重新排列得到

int_(-infty)^infty(e^(iz))/zdz=ipi,
(46)

因此

int_(-infty)^infty(sinz)/zdz=pi.
(47)

通过注意，使用 复残数 方法也得到了相同的结果

I=0+1/22piiRes_(z=0)f(z)
(48)
=ipi(z-0)(e^(iz))/z|_(z=0)
(49)
=ipi[e^(iz)]_(z=0)
(50)
=ipi,
(51)

因此

I(I)=pi.
(52)

由于被积函数是对称的，因此我们有

int_0^infty(sinx)/xdx=1/2pi,
(53)

给出在 0 处评估的 正弦积分 为

si(0)=-int_0^infty(sinx)/xdx=-1/2pi.
(54)

另请参见

Borwein 积分、傅里叶变换、傅里叶变换--矩形函数、仪器函数、Jinc 函数、Kilroy 曲线、正弦、正弦积分、Sinhc 函数、Tanc 函数

使用 Wolfram|Alpha 探索

参考文献

Baillie, R. "Advanced Problem 6241." Amer. Math. Monthly 85, 828, 1978.Baillie, R.; Henrici, P.; and Johnsonbaugh, R. "Solution to Advanced Problem 6241." Amer. Math. Monthly 87, 496-498, 1980.Bracewell, R. "The Filtering or Interpolating Function, sincx." In The Fourier Transform and Its Applications, 3rd ed. New York: McGraw-Hill, pp. 62-64, 1999.Brown, J. W. and Churchill, R. V. Fourier Series and Boundary Value Problems, 5th ed. New York: McGraw-Hill, 1993.Espinosa, O. and Moll, V. H. "On Some Definite Integrals Involving the Hurwitz Zeta Function." https://arxiv.org/abs/math/0012078. 11 Dec 2000.Finch, S. R. Mathematical Constants. Cambridge, England: Cambridge University Press, 2003.Gearhart, W. B. and Schulz, H. S. "The Function sinx/x." College Math. J. 21, 90-99, 1990. http://www.maa.org/pubs/Calc_articles/ma003.pdf.Grimsey, A. H. R. "On the Accumulation of Chance Effects and the Gaussian Frequency Distribution." Phil. Mag. 36, 294-295, 1945.Higgins, J. R. "Five Short Stories About the Cardinal Series." Bull. Amer. Math. Soc. 12, 45-89, 1985.Kac, M. Statistical Independence in Probability, Analysis and Number Theory. Washington, DC: Math. Assoc. Amer., 1959.Kogan, S. "A Note on Definite Integrals Involving Trigonometric Functions." Unpublished manuscript, n.d.McNamee, J.; Stenger, F.; and Whitney, E. L. "Whittaker's Cardinal Function in Retrospect." Math. Comput. 25, 141-154, 1971.Medhurst, R. G. and Roberts, J. H. "Evaluation of the Integral I_n(b)=(2/pi)int_0^infty(sinx/x)^ncos(bx)dx." Math. Comput. 19, 113-117, 1965.Morrison, K. E. "Cosine Products, Fourier Transforms, and Random Sums." Amer. Math. Monthly 102, 716-724, 1995.Prudnikov, A. P.; Brychkov, Yu. A.; and Marichev, O. I. Integrals and Series, Vol. 1: Elementary Functions. New York: Gordon & Breach, 1986.Sloane, N. J. A. Sequences A049330, A049331, and A118253 in "The On-Line Encyclopedia of Integer Sequences."Stenger, F. Numerical Methods Based on Sinc and Analytic Functions. New York: Springer-Verlag, 1993.Woodward, P. M. Probability and Information Theory with Applications to Radar. New York: McGraw-Hill, 1953.Zimmermann, P. "Int(sin(x)^k/x^k,x=0..infinity)." [email protected] posting, 4 Mar 1997.

在 Wolfram|Alpha 上被引用

Sinc 函数

请引用为

Weisstein, Eric W. "Sinc 函数。" 来自 MathWorld--Wolfram Web 资源。 https://mathworld.net.cn/SincFunction.html

学科分类