主题
Search

Logistic Map

下载 Mathematica 笔记本下载 Wolfram 笔记本
LogisticEquationIterations

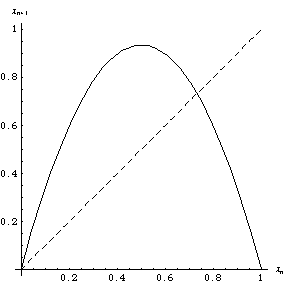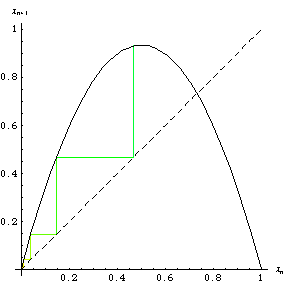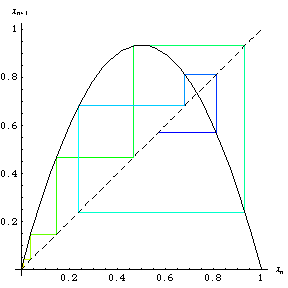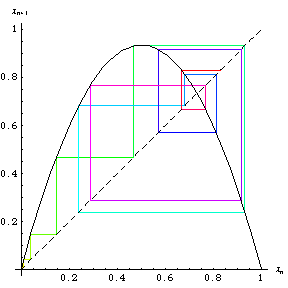
替换 logistic 方程

(dx)/(dt)=rx(1-x)
(1)

用 二次递推方程

x_(n+1)=rx_n(1-x_n),
(2)

其中 r (有时也表示为 mu) 是一个 正 常数，有时被称为“生物潜力”，给出了所谓的 logistic map。这个 二次映射 能够产生非常复杂的行为。虽然 John von Neumann 曾在 1940 年代后期建议使用 logistic map x_(n+1)=4x_n(1-x_n) 作为随机数生成器，但直到 W. Ricker 在 1954 年的工作以及 Paul Stein 和 Stanislaw Ulam 从 1950 年代开始对 logistic map 进行详细的分析研究，这种类型的映射超出简单振荡行为的复杂特性才被广泛注意到 (Wolfram 2002, pp. 918-919)。

logistic map 的前几次迭代 (2) 给出

x_1=rx_0(1-x_0)
(3)
x_2=r^2(1-x_0)x_0(1-rx_0+rx_0^2)
(4)
x_3=r^3(1-x_0)x_0(1-rx_0+rx_0^2)×(1-r^2x_0+r^2x_0^2+r^3x_0^2-2r^3x_0^3+r^3x_0^4),
(5)

其中 x_0 是初始值，上面绘制了五次迭代（迭代次数增加用颜色表示；1 为红色，2 为黄色，3 为绿色，4 为蓝色，5 为紫色），针对 r 的各种值。

Web diagram of the logistic map

使用图形程序计算的 logistic map (Tabor 1989, p. 217) 被称为 web 图。web 图 显示了这个程序的大约前一百次迭代 r=3.741 和初始值 x_0 approx 0.00079 出现在 Packel (1996; 左图) 的封面上，并在上面的右图中以动画形式展示。

通常，这个 递推方程 不能以闭合形式求解。Wolfram (2002, p. 1098) 假设任何精确解必须具有以下形式

x_n=1/2{1-f[r^nf^(-1)(1-2x_0)]},
(6)

其中 f 是某个函数，而 f^(-1) 是它的 反函数。M. Trott (私人通讯) 已经表明，对于 r 的一般值，光滑解是不存在的，r 为偶数且非零的情况可能是个例外。唯一已知的精确解是针对 r=-2、r=2 和 r=4 的情况，总结在下表中 (Wolfram 2002, p. 1098)，并且 R. Germundsson (私人通讯，2002 年 4 月 25 日) 已经证明不可能存在其他这种形式的解。

rf(x)解
-22cos(1/3(pi-sqrt(3)x))1/2-cos{1/3[pi-(-2)^n(pi-3cos^(-1)(1/2-x_0))]}
2e^x1/2{1-exp[2^nln(1-2x_0)]}
4cosx1/2{1-cos[2^ncos^(-1)(1-2x_0)]}
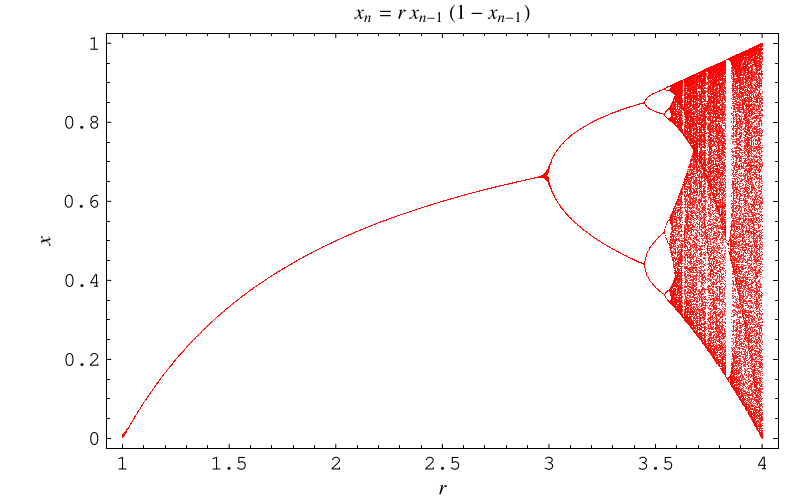
LogisticEquationBifurcation

上面的图示显示了 logistic map 的分岔图，它是通过绘制 r 的函数，一系列 x_n 的值，这些值是通过从随机值 x_0 开始，迭代多次，并丢弃与迭代收敛到吸引子之前的值对应的初始点而获得的。换句话说，对于给定的 r 值，x_n 的不动点集被绘制出来，r 的值向右递增。

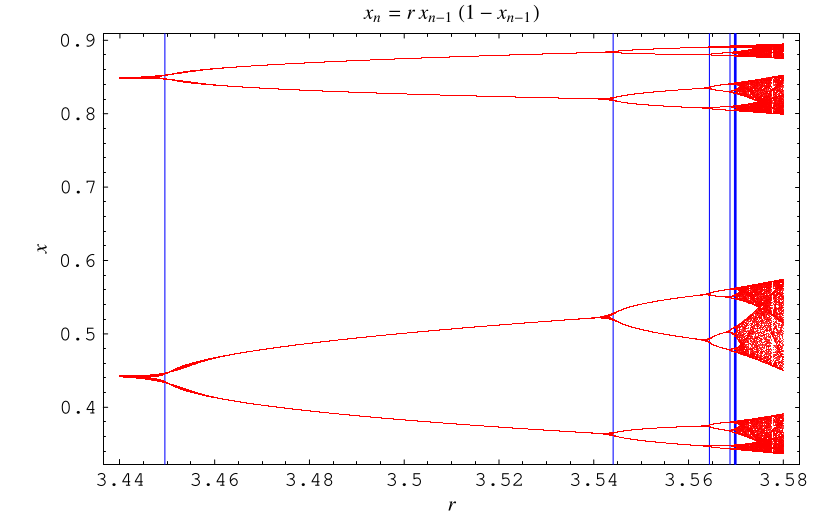
LogisticMapBifurcations

上面说明了先前图表在 r=3.5 附近的放大图，其中 r 的值，在 2^n-周期首次出现时，用蓝线标示。

为了研究 logistic map 的不动点，设初始点 x_0 位于区间 [0,1] 内。现在找到 r 的适当条件，以保持点在区间内。x_(n+1) 可以取的最大值可以从下式找到

(dx_(n+1))/(dx_n)=r(1-2x_n)=0,
(7)

因此，x_(n+1) 的最大值发生在 x_n=1/2 时。代入此值，max(x_(n+1))=r/4。因此，为了将 map 保持在期望区域内，我们必须有 r in [0,4]。雅可比矩阵是

J=|(dx_(n+1))/(dx_n)|=|r(1-2x_n)|,
(8)

如果 J(x_0)<1，则 map 在点 x_0 处是稳定的。

现在找到 map 的 不动点，当 x_(n+1)=x_n 时出现。为了方便，去掉 n 在 x_n 上的下标

f(x)=rx(1-x)=x
(9)
x[1-r(1-x)]=x(1-r+rx)=rx[x-(1-r^(-1))]=0,
(10)

因此，不动点是 x_1^((1))=0 和 x_2^((1))=1-r^(-1)。

如果选择大于 3 的 r 值，则会发生有趣的事情。map 变得不稳定，我们得到一个 音叉分岔，其中有两个周期为 2 的稳定轨道，对应于 f^2(x) 的两个稳定 不动点。二阶不动点必须满足 x_(n+2)=x_n，因此

x_(n+2)=rx_(n+1)(1-x_(n+1))
(11)
=r[rx_n(1-x_n)][1-rx_n(1-x_n)]
(12)
=r^2x_n(1-x_n)(1-rx_n+rx_n^2)
(13)
=x_n.
(14)

为了方便，去掉 n 下标并重写

x{r^2[1-x(1+r)+2rx^2-rx^3]-1}=0
(15)
x[-r^3x^3+2r^3x^2-r^2(1+r)x+(r^2-1)]=0
(16)
-r^3x[x-(1-r^(-1))][x^2-(1+r^(-1))x+r^(-1)(1+r^(-1))]=0.
(17)

请注意，我们也找到了第一个一阶 不动点，因为一阶 不动点 的两次迭代会产生一个平凡的二阶 不动点。真正的 2-周期 由二次部分的解给出

x_+/-^((2))=1/2[(1+r^(-1))+/-sqrt((1+r^(-1))^2-4r^(-1)(1+r^(-1)))]
(18)
=1/2[(1+r^(-1))+/-sqrt(1+2r^(-1)+r^(-2)-4r^(-1)-4r^(-2))]
(19)
=1/2[(1+r^(-1))+/-sqrt(1-2r^(-1)-3r^(-2))]
(20)
=1/2[(1+r^(-1))+/-r^(-1)sqrt((r-3)(r+1))].
(21)

这些解仅在 r>=3 时是 实数，因此这是 2-周期 开始的地方。请注意，2-周期也可以通过计算

(f^2(x)-x)/(f(x)-x)=r^2x^2-r(1+r)x+(1+r)=0,
(22)

的 判别式来找到，即

((1+r)(3-r))/(r^2).
(23)

当它等于 0 时，两个根重合，因此 r_2=3 是倍周期分岔的开始。对于 n=2，解 (x_1,x_2,r) 由 (0, 0, +/-1) 和 (2/3, 2/3, 3) 给出，因此第一次 分岔 发生在 r_2=3。

通常，可以求解以给出任意 n-周期开始的 n+1 个方程组 (Saha 和 Strogatz 1995) 是

{x_2=rx_1(1-x_1); x_3=rx_2(1-x_2); |; x_n=rx_(n-1)(1-x_(n-1)); x_1=rx_n(1-x_n); r^nproduct_(k=1)^(n)(1-2x_k)=1.
(24)

这些方程组的前 n 个给出 f(x)、f^2(x)、...、f^n(x)，最后一个利用了周期 n 的开始是通过 折叠分岔 发生的，因此第 n 个 导数 为 1。对于小的 n，这些方程可以精确求解，但复杂度随着 n 的增加而迅速增加。

现在寻找 3-周期 的开始。为了消除 1-周期，考虑

(f^3(x)-x)/(f(x)-x)=0.
(25)

这给出

1+r+r^2-(r^4+2r^3+2r^2+r)x+(2r^5+3r^4+3r^3+r^2)x^2-(r^6+5r^5+3r^4+r^3)x^3+(3r^6+4r^5+r^4)x^4-(3r^6-r^5)x^5+r^6x^6=0.
(26)

对于小于某个临界值 r_3 的 r，此方程的 根 都是 虚数，在这一点，其中两个根变为 实数 根。r_3 的值可以通过计算 (26) 的 判别式来找到，

D=((r^2-5r+7)^2(r^2-2r-7)^3(1+r+r^2)^2)/(r^(30)).
(27)

当 判别式 为零时，两个根重合。这发生在

r_3=1+2sqrt(2)=3.828427...
(28)

(OEIS A086178) 正如 Myrberg 在 1958 年首次展示的那样，因此 3-周期 开始于 r_3。Saha 和 Strogatz (1995) 给出了 3-周期的简化代数处理方法，其中包括求解

r^3(1-2alpha+4beta-8gamma)=1,
(29)

以及其他三个联立方程，其中

alpha=x_1+x_2+x_3
(30)
beta=x_1x_2+x_1x_3+x_2x_3
(31)
gamma=x_1x_2x_3.
(32)

Bechhoeffer (1996) 和 Gordon (1996) 仍提供了进一步的简化，但这些技术都不能容易地推广到更高的 周期。Bechhoeffer (1996) 将这三个附加方程表示为

2alpha=3+r^(-1)
(33)
4beta=3/2+5r^(-1)+3/2r^(-2)
(34)
8gamma=-1/2+7/2r^(-1)+5/2r^(-2)+5/2r^(-3),
(35)

给出

r^2-2r-7=0.
(36)

这具有先前找到的正解，r_3=1+2sqrt(2)。

Gordon (1996) 不仅推导出了 3-周期 开始的值，还推导出了一个上限 r^'，用于支持稳定周期 3 轨道的 r-值。该值与 三次方程 的唯一正根 s_1 相关

s^3-11s^2+37s-108=0
(37)

通过

r^'=1+sqrt(s_1),
(38)

这是六次多项式的唯一正 根

r^'=(x^6-6x^5+4x^4+24x^3-14x^2-36x-81)_2
(39)
=3.841499007543...
(40)

(OEIS A086179)。对于 n=3,

(d[f^3(x)])/(dx)=(d[f^3(x)])/(d[f^2(x)])(d[f^2(x)])/(d[f(x)])(d[f(x)])/(dx)
(41)
=(d[f(z)])/(dz)(d[f(y)])/(dy)(d[f(x)])/(dx)
(42)
=r^3(1-2z)(1-2y)(1-2x).
(43)

使用计算机代数求解得到的三次 三次方程 给出

r=1+2sqrt(2)
(44)

以及由下式给出的 x_1、x_2、x_3

343x^6-980x^5+868x^4-134x^3-161x^2+70x-7=0,
(45)

给出数值根

x_1=(343x^6-980x^5+868x^4-134x^3-161x^2+70x-7)_2
(46)
=sqrt(2)-2/7(1-2sqrt(2))[1+cos(2/7pi)-5]
(47)
=0.514355...
(48)
x_2=(343x^6-980x^5+868x^4-134x^3-161x^2+70x-7)_4
(49)
=sqrt(2)-2/7(1-2sqrt(2))[1+cos(4/7pi)-5]
(50)
=0.956318...
(51)
x_3=(343x^6-980x^5+868x^4-134x^3-161x^2+70x-7)_5
(52)
=sqrt(2)-2/7(1-2sqrt(2))[1+cos(6/7pi)-5]
(53)
=0.159929...
(54)
r=3.828427...,
(55)

其中 2+2cos(2/7pi) 是 白银常数。

为了找到 4-周期 的开始，通过考虑以下因素来消除 2-周期和 1-周期

(f^4(x)-x)/(f^2(x)-x)=0.
(56)

这给出了 x 的 12 阶多项式。r_4 的值可以通过计算这个多项式的 判别式来找到，

D=((r^2+1)^3(r^2-4r+5)^3(r^2-2r-5)^2)/(r^(132))(r^6-6r^5+3r^4+28r^3-9r^2-54r-135),
(57)

其唯一的实数正根是

r_4^'=1+sqrt(6)
(58)
=3.449489...
(59)
r_4^('')=1+sqrt(4+3(4^(1/3)))
(60)
=3.906010...
(61)

因此，4-周期 开始于

r_4=1+sqrt(6)=3.449489...
(62)

(OEIS A086180)。

可以通过解析方法找到 5-周期的开始，并给出一个 r 的 22 阶多项式，其真实的实数正根是 r_5=3.73817... (OEIS A118452)、3.90557... 和 3.99026....

可以通过解析方法找到 6-周期的开始，并给出一个 r 的 40 阶多项式，其真实的实数正根是 r_6=3.62655... (OEIS A118453)、3.93751...、3.97776... 和 3.99758....

可以通过解析方法找到 7-周期的开始，并给出一个 r 的 114 阶多项式，其真实的实数正根是 r_7=3.70164... (OEIS A118746)、3.77413...、3.88602...、3.92218...、3.95102...、3.96897...、3.98474...、3.99453... 和 3.99939....

可以通过解析方法找到 8-周期的开始，它是 8 阶多项式的 多项式根

r_8=(4913+2108t^2-604t^3-977t^4+8t^5+44t^6+392t^7-193t^8-40t^9+48t^(10)-12t^(11)+t^(12))_3
(63)
=3.54409...
(64)

(OEIS A086181; Bailey 1993; Bailey and Broadhurst 2000; Borwein and Bailey 2003, pp. 51-52)。

最初使用 整数关系 计算找到了 r_(16)=3.564407266095... (OEIS A091517) 处 16-周期的开始，该计算确定 alpha=r_(16)(r_(16)-2) 是一个 120 次 整系数多项式 的根，其系数从 257^(30) 单调递减到 1 (Bailey 和 Broadhurst 2000; Borwein 和 Bailey 2003, pp. 52-53)。随后使用计算机代数精确地验证了这一结果 (Borwein 和 Bailey 2003, p. 53; Kotsireas 和 Karamanos 2004)，并且是一个 240 次的 代数数。

下表总结了 r_n 值，在该值处 n-周期首次出现。对于 n=1、2、...，这些值的代数次数为 1、1、2、2、22、40、114、12、... (OEIS A118454)。

ndeg(r_n)OEIS值
111
213
32A0861783.82842712...
42A0861803.44948974...
522A1184523.73817237...
640A1184533.62655316...
7114A1187463.70164076...
812A0861813.54409035...
9
10
16240A0915173.56440726...

r_(2^n) 值的代数阶数（即，2^n-周期的开始）对于 n=1、2、...，因此由 1、2、12、240、... 给出 (OEIS A087046)。下表给出了周期类型和 r_(2^n) 值，在该值处周期 2^n 出现。

n周期 (2^n)r_(2^n)OEIS
123
243.449490A086180
383.544090A086181
4163.564407A091517
5323.568750
6643.56969
71283.56989
82563.569934
95123.569943
1010243.5699451
1120483.569945557
infty累积点3.569945672A098587

有关其他值，请参见 Rasband (1990, p. 23)。请注意，Tabor (1989, p. 222) 中的表格是不正确的，Lauwerier (1991) 中的 n=2 条目也是不正确的。倍周期 分岔 变得越来越快 (8, 16, 32, ...)，然后突然中断。超过某个被称为 累积点 的点后，周期性让位于 混沌，如下所示。在复杂性的中间，由于 模式锁定，突然出现一个具有规则周期（如 3 或 7）的窗口。3-周期 分岔发生在 r=1+2sqrt(2)=3.828427...，并且 倍周期分岔 然后再次开始，周期为 6、12、... 和 7、14、28、...，然后再次中断为 混沌。但是，请注意，可以在这种混沌中找到相当大的结构 (Mayoral 和 Robledo 2005ab)。

相对容易证明，对于 r>2+sqrt(5) approx 4.236 (Devaney 1989, pp. 31-50; Gulik 1992, pp. 112-126; Holmgren 1996, pp. 69-85)，logistic map 在不变 Cantor 集 上是 混沌 的，但事实上，对于所有 r>4 (Robinson 1995, pp. 33-37; Kraft 1999)，它也是 混沌 的。

logistic map 具有 关联指数 0.500+/-0.005 (Grassberger 和 Procaccia 1983)、容量维数 0.538 (Grassberger 1981) 和 信息维数 0.5170976 (Grassberger 和 Procaccia 1983)。

logistic map 可以用来生成随机数 (Umeno 1998; Andrecut 1998; Gonzáles 和 Pino 1999, 2000; Gonzáles et al. 2001ab; Wong et al. 2001, Trott 2004, p. 105)。

另请参阅

2x mod 1 映射, 分岔, 费根鲍姆常数, Logistic Map--r=2, Logistic Map--r=2, Logistic Map--r=4, 周期三定理, 二次映射, 白银常数, 帐篷映射

使用 Wolfram|Alpha 探索

参考文献

Bailey, D. H. “多精度 Fortran 程序的翻译和执行。” ACM 数学软件汇刊 19, 288-319, 1993。Bailey, D. H.; Borwein, J. M.; Calkin, N. J.; Girgensohn, R.; Luke, D. R.; 和 Moll, V. H. “混沌理论中的分岔点。” §2.3.2 in 实验数学行动。 Wellesley, MA: A K Peters, pp. 33-36, 2007。Bailey, D. H.; Borwein, J. M.; Kapoor, V.; 和 Weisstein, E. W. “实验数学中的十个问题。” 美国数学月刊 113, 481-509, 2006。Bailey, D. H. 和 Broadhurst, D. J. “并行整数关系检测：技术与应用。” 数学计算 70, 1719-1736, 2000。Bechhoeffer, J. “周期 3 的诞生，再访。” 数学杂志 69, 115-118, 1996。Beck, C.; 和 Schlögl, F. 混沌系统热力学。 英国剑桥: 剑桥大学出版社, 1993。Bogomolny, A. “混沌的创造（混沌中存在秩序）。” http://www.cut-the-knot.org/blue/chaos.shtml。Borwein, J. 和 Bailey, D. “Logistic 迭代中的分岔点。” §2.3 in 实验数学：21 世纪的合理推理。 Wellesley, MA: A K Peters, pp. 50-53, 2003。Costa, U. M. S.; Lyra, M. L.; Plastino, A. R.; 和 Tsallis, C. “Logistic 类映射族中对初始条件的幂律敏感性：分形性和非广延性。” 物理评论 E 56, 245-250, 1997。Devaney, R. 混沌动力系统导论，第 2 版。 Redwood City, CA: Addison-Wesley, 1989。Dickau, R. M. “分岔图。” http://mathforum.org/advanced/robertd/bifurcation.html。Elaydi, S. N. 离散混沌。 Boca Raton, FL: Chapman & Hall, 2000。Gleick, J. 混沌：一门新科学的诞生。 纽约: Penguin Books, pp. 69-80, 1988。Gordon, W. B. “Logistic 映射的周期三轨道。” 数学杂志 69, 118-120, 1996。Grassberger, P. “分形吸引子的 Hausdorff 维数。” 统计物理学杂志 26, 173-179, 1981。Grassberger, P. 和 Procaccia, I. “测量奇异吸引子的奇异性。” 物理 D 9, 189-208, 1983。Gulick, D. 混沌相遇。 纽约: McGraw-Hill, 1992。Holmgren, R. 离散动力系统第一课程，第 2 版。 纽约: Springer-Verlag, 1996。Mathematica Jaffe, S. “Logistic 方程：可计算的混沌。” http://library.wolfram.com/infocenter/MathSource/579/。Kotsireas, I. S. 和 Karamanos, K. “Logistic 映射的分岔点 b_4 和 Bailey-Broadhurst 猜想的精确计算。” 国际分岔与混沌杂志 14, 2417-2423, 2004. http://www.lacim.uqam.ca/~plouffe/OEIS/archive_in_pdf/costas-cecm.pdfKraft, R. L. “Logistic 映射的混沌、康托集和双曲性。” 美国数学月刊 106, 400-408, 1999。Latora, V.; Rapisarda, A.; Tsallis, C.; 和 Baranger, M. “混沌边缘熵增加率。” 物理快报 A 273, 97, 2000。Lauwerier, H. 分形：无限重复的几何图形。 Princeton, NJ: Princeton University Press, pp. 119-122, 1991。MathPages. “Logistic 映射的闭合形式。” http://www.mathpages.com/home/kmath188.htm。May, R. M. “具有非常复杂动力学的简单数学模型。” 自然 261, 459-467, 1976。Mayoral, E. 和 Robledo, A. “近期对混沌边缘奇异动力学的赏析。” 2005 年 1 月 17 日。 http://arxiv.org/abs/cond-mat/0501398。Mayoral, E. 和 Robledo, A. “Tsallis' q 指数和 Mori's q 混沌边缘的相变。” 物理评论 E 72, 026209, 2005b。Packel, E. 面向数学教师的 Mathematica。 计算研究所, 1996。Pearl, R. 第 18 章 in 人口增长的生物学。 纽约: Knopf, 1978。Peitgen, H.-O.; Jürgens, H.; 和 Saupe, D. 混沌与分形：科学的新领域。 纽约: Springer-Verlag, pp. 585-653, 1992。Quetelet, A. 和 Verhulst, P. F. 比利时皇家科学院年鉴 16, 97-124, 1850。Ramasubramanian, K. 和 Sriram, M. S. “使用不同算法计算 Lyapunov 谱的比较研究。” 1999 年 9 月 17 日。 http://arxiv.org/abs/chao-dyn/9909029。Rasband, S. N. 非线性系统的混沌动力学。 纽约: Wiley, p. 23, 1990。Robinson, C. 稳定性、符号动力学和混沌。 Boca Raton, FL: CRC Press, 1995。Russell, D. A.; Hanson, J. D.; 和 Ott, E. “奇异吸引子的维度。” 物理评论快报 45, 1175-1178, 1980。Saha, P. 和 Strogatz, S. H. “周期三的诞生。” 数学杂志 68, 42-47, 1995。Sloane, N. J. A. 序列 A086178, A086179, A086180, A086181, A087046, A091517, A098587, A118452, A118453, A118454, 和 A118746 在“整数序列在线百科全书”中。Strogatz, S. H. 非线性动力学与混沌。 Reading, MA: Addison-Wesley, 1994。Tabor, M. 非线性动力学中的混沌与可积性：导论。 纽约: Wiley, 1989。Tsallis, C.; Plastino, A. R.; 和 Zheng, W.-M. “对初始条件的幂律敏感性——新的熵表示。” 混沌、孤子与分形 8, 885-891, 1997。Trott, M. Mathematica 编程指南。 纽约: Springer-Verlag, pp. 24-25, 2004. http://www.mathematicaguidebooks.org/。Wagon, S. “二次映射的动力学。” §4.4 in Mathematica 行动。 纽约: W. H. Freeman, pp. 117-140, 1991。Wolfram Research, Inc. “Logistic 映射。” http://documents.wolfram.com/mathematica/Demos/SoundGallery/LogisticMap.html。Wolfram, S. 一种新的科学。 Champaign, IL: Wolfram Media, pp. 918-921 和 1098, 2002。

在 Wolfram|Alpha 中被引用

Logistic Map

请按如下方式引用

Weisstein, Eric W. “Logistic 映射。” 来自 MathWorld——Wolfram Web 资源。 https://mathworld.net.cn/LogisticMap.html

学科分类