多项式根

多项式 的根是一个数 ，使得 。 代数基本定理指出，一个 多项式 ，其次数为 ，有 个根，其中一些可能是重根。例如，多项式

(1)

的根是 、1 和 2。因此，求多项式的根等价于将多项式 因式分解 为 1 次因式。

任何 多项式 都可以进行数值因式分解，尽管不同的 算法 有不同的优点和缺点。

多项式方程的根可以在 Wolfram 语言 中使用以下命令精确找到：Roots[lhs==rhs, var]，或者使用以下命令进行数值求解：NRoots[lhs==rhs, var]。一般而言，多项式 的给定根表示为Root[#^n+a[n-1]#^(n-1)+...+a[0]&, k]，其中 , 2, ..., 是标识特定根的索引，而纯函数多项式是 不可约的。请注意，在 Wolfram 语言 中，根的排序在以下每个命令中都不同：Roots, NRoots, 以及Table[Root[p, k], k, n]。

在 Wolfram 语言 中，涉及Root对象的代数表达式可以使用以下命令组合成新的Root对象：RootReduce.

在这项工作中，多项式 的第 个根在 Wolfram 语言 的Root对象的排序中表示为 ，其中 是一个哑变量。在这种排序中，实根排在复根之前，并且 复共轭 根对是相邻的。例如，

			(2)
			(3)

和

			(4)
			(5)
			(6)

设多项式

(7)

的 根 表示为 、 、 ...、 。那么 韦达定理 给出

			(8)
			(9)
			(10)

这些可以通过写出

(11)

展开，然后将系数与 (◇) 进行比较来推导出来。

给定一个 次多项式 ，可以通过找到 矩阵

(12)

的 特征值 来找到 根，并取 。这种方法计算量可能很大，但对于查找接近和多重根非常稳健。

如果 多项式

(13)

的 系数 被指定为 整数，那么有理根的 分子 必须是 的因子，而 分母 必须是 的因子（符号可以是正负）。这被称为 多项式余数定理。

如果一个 多项式 没有 负 根（可以通过 笛卡尔符号法则 确定），那么 最大下界 为 0。否则，写出 系数，设 ，并计算下一行。现在，如果任何 系数 为 0，则将它们设置为负的下一个更高阶 系数 的符号，从第二高阶 系数 开始。如果所有符号交替，则 是最大下界。如果不是，则从 中减去 1，并计算另一行。例如，考虑 多项式

(14)

执行上述 算法 然后给出

0	2	2		1
	2	0		8
--	2			8
	2			7
	2		5		35

因此，最大下界是 。

如果一个 多项式 没有 正 根（可以通过 笛卡尔符号法则 确定），那么 最小上界 为 0。否则，写出 多项式 的 系数，必要时包括零。设 。在下一行，写出最高阶 系数。从第二高阶 系数 开始，将 乘以刚刚写出的数字加到原始的第二个 系数，并将其写在第二个 系数 下面。继续到零阶。如果所有 系数 都是 非负的，则最小上界是 。如果不是，则将 加一，然后再次重复该过程。例如，取 多项式

(15)

执行上述 算法 给出

0	2			1
1	2	1
2	2	3
3	2	5	8	25	68

因此，最小上界 是 3。

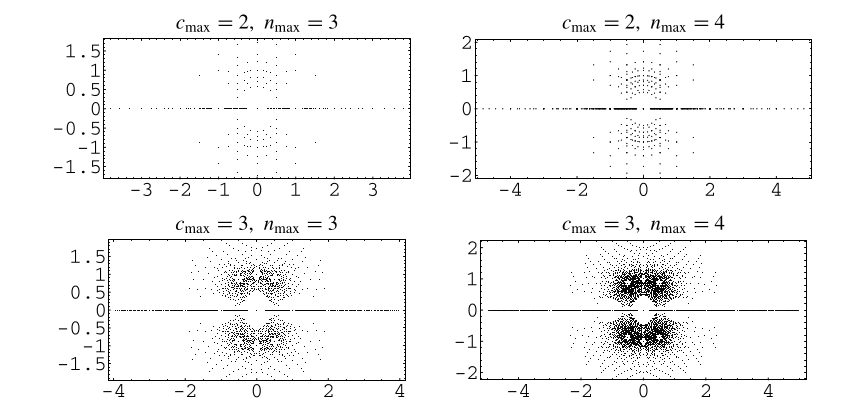
在复平面上绘制所有次数不超过某个次数且整数系数的绝对值小于某个截止整数的多项式的根，显示了上面所示的美丽结构（Trott 2004，第 23 页）。

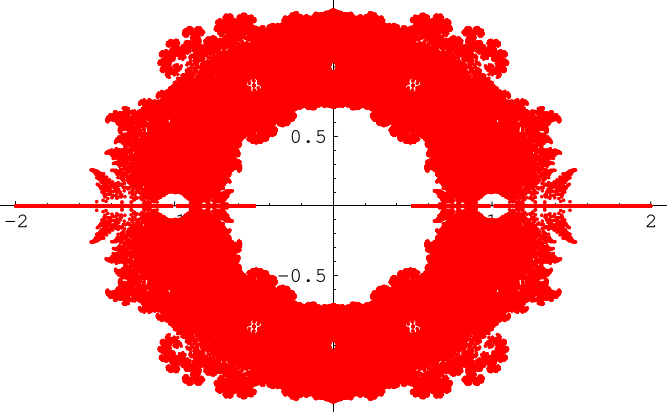
通过绘制所有系数为 且次数高达 的所有多项式的根，可以获得更令人惊叹的图形（Borwein 和 Jörgenson 2001；Pickover 2002；Bailey 等人 2007，第 18 页）。