基本群

一个弧连通集 的基本群是由所有环路的集合的等价类形成的群，即，起点和终点都在给定的基点 的路径，在同伦的等价关系下。这个群的单位元是所有与由点 组成的退化路径同伦的所有路径的集合。同胚空间的基群是同构的。事实上，基本群只取决于 的同伦型。拓扑空间的基本群由庞加莱引入（Munkres 1993, p. 1）。

以下是一些常见空间 的基本群表格，其中 表示基本群， 是第一个整同调群， 表示群直积， 表示自由积， 表示整数环，并且 是 阶的循环群。

空间 ()	符号
圆
复射影空间		0	0
8字形
克莱因瓶
-环面
实射影平面
球面		0	0

环路 和 环路 的群乘积 由 的路径之后跟随 的路径给出。单位元由常路径表示，而 的逆元通过沿相反方向遍历 给出。基本群与基点的选择无关，因为通过 的任何环路都与通过任何其他点 的环路同伦。因此，说“ 的基本群”是有意义的。

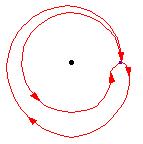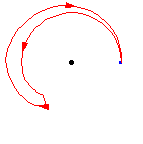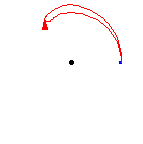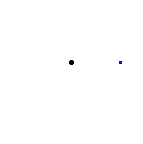
上面的图表显示，一个环路后跟相反的环路与常环路同伦，即，单位元。也就是说，它首先遍历路径 ，然后调头并沿另一条路返回，。组合被变形或同伦到常路径，沿着原始路径 。

具有平凡基本群（即，每个环路都与常环路同伦）的空间称为单连通的。例如，任何可收缩空间，如欧几里得空间，都是单连通的。球面是单连通的，但不是可收缩的。根据定义，万有覆叠空间 是单连通的，并且 中的环路提升为 中的路径。万有覆叠空间中提升的路径定义了覆盖变换，它们形成一个与基本群同构的群。

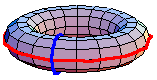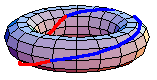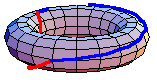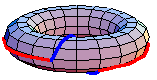
的基本群的底层集合是从圆到 的基于基点的同伦类的集合，表示为 。对于一般的空间 和 ，在 上没有自然的群结构，但是当存在时， 被称为余-H-空间。除了圆之外，每个超球面 都是一个余-H-空间，定义了同伦群。一般来说，基本群是非阿贝尔群。然而，更高阶的同伦群是阿贝尔群。在一些特殊情况下，基本群是阿贝尔群。例如，上面的动画显示了在环面中 。红色路径在蓝色路径之前进行。该动画是首先绕内部环的环路和首先绕外部环的环路之间的同伦。

由于第一个整数同调 也由环路表示，环路是唯一没有边界的一维对象，因此存在群同态

它是满射的。事实上， 的群核是换位子群，并且 被称为阿贝尔化。

当 可以写成基本群已知的空间的并集 时，可以使用 范·坎彭定理 计算 的基本群。

当 是连续映射时，基本群向前推送。也就是说，存在一个映射 ，其定义为取自 的环路的图像。前推映射是自然的，即，每当定义两个映射的组合时，。