同伦群将基本群推广到来自更高维度球体的映射,而不是来自圆的映射。阶同伦群,对于拓扑空间
,是来自n-维球面到
的映射的同伦类的集合,具有群结构,并表示为
。基本群是
,并且,如在
的情况下,映射
必须通过基点
。对于
,同伦群
是一个阿贝尔群。
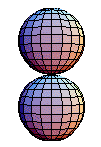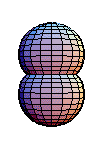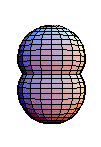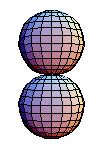
群运算不像基本群的运算那样简单。考虑两个映射 和
,它们都通过
。乘积
通过将赤道映射到基点
给出。然后将北半球通过将赤道坍缩为一个点映射到球面,然后再通过
映射到
。南半球类似地通过
映射到
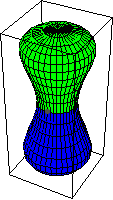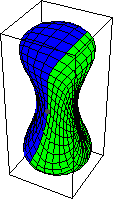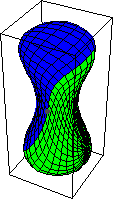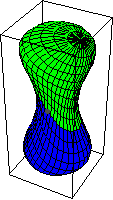
。上面的图示显示了两个球面的乘积。

单位元由常值映射 表示。基本群中环路方向的选择对应于同伦群中
的流形定向。因此,映射
的逆映射通过切换球面的定向给出。通过在
坐标中描述球面,切换第一和第二坐标会改变球面的定向。或者作为超曲面,
,切换定向会反转内部和外部的角色。上面的图示表明
与常值映射同伦,即单位元。它首先通过扩展
中的赤道开始,然后将结果映射收缩到基点。
与基本群一样,同伦群不依赖于基点的选择。但是,高阶同伦群始终是阿贝尔群。上面的图示显示了 的一个示例。基点是固定的,并且因为
映射可以旋转。当
,即基本群时,在保持基点固定的同时旋转映射是不可能的。
对于所有 ,
的空间称为
-连通的。如果
是
-连通的,
,那么从
阶同伦群到
阶同调群的胡列维茨同态
是一个同构。
当 是一个连续映射时,则通过取
下的像来定义
,其中像是
中的球面。前推是自然的,即,只要定义了两个映射的组合,
。实际上,给定一个纤维化,