覆盖变换

覆盖变换，也称为覆盖空间变换，对于任何覆盖 都有定义。它们通过同胚作用于 ，这些同胚保持投影 。覆盖变换可以通过提升从空间 到其万有覆盖 的路径来定义，万有覆盖是一个单连通空间，并且是 的覆盖。 中的每个环路，比如单位区间上的函数 ，其中 ，提升为 中的路径，它仅取决于 的选择，即 的原像中的起始点。此外，端点 仅取决于 的同伦类和 。给定一个点 ，以及 ， 的基本群的一个元素，点 被定义为表示 的路径 的提升的端点。

万有覆盖 的覆盖变换形成一个群 ，它是商空间的基本群

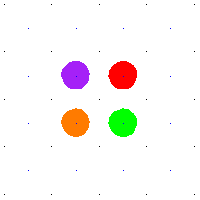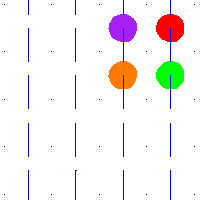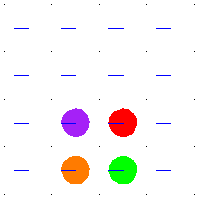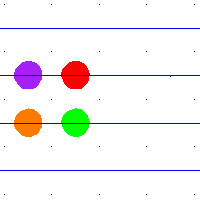
例如，当 是平方环面时，那么 是平面，并且原像 是整数格点 的平移。环面中的任何环路都提升到平面中的路径，其端点位于整数格点中。这些平移的整数格点是 在 上通过加法作用的群轨道。上面的动画展示了一些覆盖变换在平面上的一些圆盘上的作用。空间是环面及其万有覆盖，即平面。基本群的一个元素（蓝色路径所示）定义了万有覆盖的一个覆盖变换。它在万有覆盖中移动点。移动后的点在环面中有相同的投影。蓝色路径是环面上的一个环路，并显示了它的所有原像。