设 
为一个 群，并设 
为群元素的集合，使得 单位元 
。与 
关联的凯莱图被定义为 有向图，其顶点与每个群元素关联，且有有向边 
，每当 
时。凯莱图可能取决于生成集的选择，并且是 连通的 当且仅当 
生成 
（即，集合 
是 
的 群生成元）。
需要注意的是，术语“凯莱图”也用于 
被隐式地理解为群的生成元集合时，在这种情况下，图总是连通的（但通常，仍然取决于生成元的选择）。群 
的这种凯莱图可以使用 Wolfram 语言 计算，使用CayleyGraph[G]，其中使用的生成元是那些由以下命令返回的生成元GroupGenerators[G]。
更复杂的是，适当有向凯莱图的无向版本也被称为凯莱图。
特定生成元集合的 交错群 
的无向凯莱图有时被称为 交错群图。循环群 
的凯莱图是 圈图 
，而 二面体群 
的凯莱图是 棱柱图 
。其他属于凯莱图的图类包括 循环图（如果需要生成集则连通；如果不要求则可能不连通）、立方体连接环、汉明图 和 超立方体图。
有向图凯莱图的每个节点的 边重数 相同。（有向或无向）凯莱图始终是 顶点传递图，但反之不一定成立。然而，在小型 顶点传递图 中，很大一部分是凯莱图（McKay 和 Royle 1990）。
Royle 维护了一个非必要连通的顶点传递图列表，其中包含顶点数最多为 31 的凯莱图或非凯莱图的指定，尽管对于 27、28 和 30 个顶点的值尚未经过独立验证（尽管群中的错误只会影响图，如果以某种方式遗漏了最小传递群，因此不太可能出现错误）。顶点数为 
, 2, ... 的非必要连通凯莱图的数量分别为 1, 2, 2, 4, 3, 8, 4, 14, 9, 20, 8, 74, ... （OEIS A185959；McKay 和 Royle 1990，McKay 和 Praeger 1994），以及存在非凯莱顶点传递图的顶点数分别为 10, 15, 16, 18, 20, 24, 26, 28, 30, ....
最小的顶点传递非凯莱图是 彼得森图 
（McKay 和 Praeger 1994），而最小的非连通顶点传递非凯莱图是两个 
的副本。
凯莱图可以通过从生成元排列集合 
（不包括单位排列）开始生成，并相互排列元素直到不再有新的排列产生。这会产生一个在元素排列下闭合的集合 
。如果对于某些 
，
成立，则连接每对排列 
与一条边，然后得到一个凯莱图。
唯一可以给出平面凯莱图的群恰好是 
、
、
、
、
和 
，正如 Maschke (1896) 所证明的那样。
下表列出了一些由少量小排列生成的凯莱图的无向版本。
| 图 | 生成元 |
| 16-胞 图 |   1,2,4,3 ,  2,1,3,4 ,  2,1,4,3 ,  3,4,1,2 ,  3,4,2,1  |
循环图  |   1,2,3,5,4 ,  1,2,4,3,5 ,  2,1,3,5,4 ,  2,1,5,4,3  |
完全二分图  |   1,2,4,3 ,  2,1,3,4 ,  3,4,2,1  |
  1,2,4,3 ,  2,1,3,4 ,  3,4,1,2 ,  4,3,2,1  | |
  1,2,4,5,6,3 ,  2,1,4,5,6,3  | |
完全图  |   1,3,2 ,  2,1,3 ,  2,3,1 ,  3,2,1  |
  1,2,4,3 ,  1,3,2,4 ,  1,3,4,2 ,  1,4,3,2  | |
  1,2,4,3 ,  1,3,2,4 ,  1,3,4,2 ,  1,4,2,3 ,  1,4,3,2  | |
| 立方图 |   1,2,4,3 ,  3,4,2,1  |
  1,2,4,3 ,  2,1,3,4 ,  3,4,1,2  | |
  1,2,3,5,4 ,  1,4,5,3,2  | |
立方对称图  |   1,2,4,3 ,  1,3,2,4 ,  3,2,1,4  |
  1,2,3,4,6,5 ,  2,5,4,6,3,1  | |
立方对称图  |   1,3,2,5,4 ,  2,1,4,3,5 ,  4,5,3,1,2  |
| 立方顶点传递图 Ct19 |   1,2,3,4,6,5 ,  1,2,4,3,6,5 ,  5,6,3,4,1,2  |
| 立方顶点传递图 Ct23 |   1,2,3,4,6,5 ,  2,3,1,5,6,4  |
| 立方顶点传递图 Ct28 |   1,3,2,5,4 ,  2,3,4,1,5  |
| 立方顶点传递图 Ct37 |   1,2,4,3 ,  1,3,2,4 , 3,4,1,2  |
| 立方顶点传递图 Ct38 |   1,2,3,4,5,7,6 ,  2,3,1,6,7,4,5  |
| 立方顶点传递图 Ct41 |   1,2,4,3 ,  1,3,2,4 , 2,1,4,3  |
| 立方顶点传递图 Ct42 |   1,2,3,4,5,7,6 ,  2,3,4,1,6,5,7  |
| 立方八面体图 |   1,3,4,2 ,  2,3,1,4  |
  1,3,4,2 ,  1,4,2,3 ,  2,3,1,4  | |
  1,3,4,2 ,  1,4,2,3 ,  2,3,1,4 ,  3,1,2,4  | |
  1,2,4,5,3 ,  1,3,4,2,5  | |
| 5-圈图 |   2,3,4,5,1 ,  5,1,2,3,4  |
| 6-圈图 |   1,3,2 ,  2,1,3  |
  1,2,4,3 ,  1,3,2,4  | |
  1,2,3,5,4 ,  1,2,4,3,5  | |
| 8-圈图 |   1,2,4,3 ,  3,4,1,2  |
  1,2,3,5,4 ,  1,4,5,2,3  | |
| 10-圈图 |   1,3,2,5,4 ,  2,1,4,3,5  |
| 12-圈图 |   1,2,3,5,4 ,  2,1,4,3,5  |
| 富兰克林图 |   1,2,3,5,4 ,  1,2,4,3,5 ,  2,1,3,5,4  |
  1,2,3,4,5,7,6 ,  1,2,3,4,6,5,7 ,  1,2,4,3,5,7,6  | |
| 大斜方立方八面体图 |   1,2,3,4,5,7,6 ,  1,2,3,4,6,5,7 ,  1,3,2,5,4,7,6  |
| 二十面体图 |   1,3,4,2 ,  2,1,4,3 ,  2,3,1,4  |
  1,3,4,2 ,  1,4,2,3 ,  2,1,4,3 ,  2,3,1,4  | |
  1,3,4,2 ,  1,4,2,3 ,  2,1,4,3 ,  2,3,1,4 ,  3,1,2,4  | |
| 4-莫比乌斯梯子 |   1,2,4,3 ,  2,1,4,3 ,  3,4,1,2  |
| 八面体图 |   1,3,2 ,  2,1,3 ,  2,3,1  |
  1,2,4,3 ,  1,3,2,4 ,  1,3,4,2  | |
  1,2,4,3 ,  1,3,2,4 ,  1,3,4,2 ,  1,4,2,3  | |
  1,2,4,5,3 ,  2,1,4,5,3  | |
  1,2,4,5,3 ,  2,1,4,5,3  | |
| 帕普斯图 |   1,2,3,4,6,5 ,  2,3,1,5,4,6  |
| 2-路径图 |   2,1  |
  1,3,2  | |
| 五胞体 图 |   2,3,4,5,1 ,  3,4,5,1,2  |
| 5-棱柱图 |   1,3,2,5,4 ,  2,4,1,5,3  |
  1,3,2,5,4 ,  2,4,1,5,3  | |
| 6-棱柱图 |   1,2,3,5,4 ,  2,1,4,5,3  |
  1,2,3,5,4 ,  2,1,4,5,3  | |
| 小斜方二十面十二面体图 |   1,2,4,5,3 ,  3,4,2,5,1  |
| 小斜方立方八面体图 |   1,3,4,2 ,  2,3,4,1  |
  1,3,4,2 ,  1,4,2,3 ,  2,3,4,1  | |
  1,3,4,2 ,  1,4,2,3 ,  2,3,4,1 ,  4,1,2,3  | |
  1,2,4,5,3 ,  1,3,4,5,2  | |
| 扭棱立方图 |   1,2,4,3 ,  2,3,1,4 ,  2,3,4,1  |
  1,2,4,3 ,  2,3,1,4 ,  2,3,4,1 ,  3,1,2,4  | |
  1,2,4,3 ,  2,3,1,4 ,  2,3,4,1 ,  3,1,2,4 ,  4,1,2,3  | |
| 正方形 反棱柱图 |   1,2,4,3 ,  3,4,1,2 ,  3,4,2,1  |
  1,2,4,3 ,  3,4,1,2 ,  3,4,2,1 ,  4,3,1,2  | |
| 正方图 |   1,2,4,3 ,  2,1,3,4  |
  1,2,3,5,4 ,  1,3,2,4,5  | |
| 超立方体图 |   1,2,3,4,6,5 ,  1,2,4,3,5,6 ,  3,4,2,1,5,6  |
| 四面体图 |   2,1,4,3 ,  3,4,2,1  |
  1,2,4,3 ,  2,1,3,4 ,  2,1,4,3  | |
  1,3,2,5,4 ,  1,4,5,3,2  | |
| 三角形图 |   2,3,1  |
  1,3,4,2 ,  1,4,2,3  | |
  1,2,4,5,3 ,  1,2,5,3,4  | |
| 三角 棱柱图 |   1,3,2 ,  2,3,1  |
  1,2,4,3 ,  1,3,4,2  | |
  1,2,4,3 ,  1,3,4,2 ,  1,4,2,3  | |
  1,2,3,5,4 ,  1,2,4,5,3  | |
| 截角立方体图 |   1,2,4,3 ,  2,3,1,4  |
  1,2,4,3 ,  2,3,1,4 ,  3,1,2,4  | |
  1,2,3,5,4 ,  1,3,4,2,5  | |
| 截角十二面体图 |   1,2,4,5,3 ,  3,4,1,2,5  |
| 截角二十面体图 |   1,3,2,5,4 ,  2,3,4,5,1  |
| 截角八面体图 |   1,2,4,3 ,  2,3,4,1  |
  1,2,4,3 ,  1,3,2,4 ,  2,1,3,4  | |
  1,2,3,5,4 ,  1,3,4,5,2  | |
| 截角四面体图 |   1,3,4,2 ,  2,1,4,3  |
  1,3,4,2 ,  1,4,2,3 ,  2,1,4,3  | |
  1,2,4,5,3 ,  1,3,2,5,4  | |
效用图  |   1,3,2 ,  2,1,3 ,  3,2,1  |
  1,2,4,3 ,  1,3,2,4 ,  1,4,3,2  | |
  1,2,3,5,4 ,  2,3,1,5,4  | |
  1,2,3,5,4 ,  2,3,1,5,4  |
例如，二面体群 
是一个 14 个元素的 置换群，它可以由分别对应于反转和旋转的两个元素生成。因此，任何两个这样的元素都会给出一个具有 14 个节点和 28 条边的连通凯莱图。上面的左图显示了生成器选择为 (7, 1, 2, 3, 4, 5, 6) 和 (7, 6, 5, 4, 3, 2, 1) 的凯莱图，其中反转以红色显示，旋转以蓝色显示。任何两个仅对应于旋转的元素将给出一个不连通的图，并且恰好有 15 对这样的元素，因为有 
种方法从六个可能的旋转中选取两个元素。（这里，数字 6 而不是 7 出现，因为单位元素可能不是给出凯莱图的子集的成员。）右图显示了由元素 (7, 1, 2, 3, 4, 5, 6) 和 (6, 7, 1, 2, 3, 4, 5) 生成的 
的凯莱图，该图是不连通的，因为这些元素不生成该群（特别是，在没有翻转的情况下，正阶排列无法切换到负阶；因此获得两个独立的环）。
上图显示了使用元素 (2, 1, 4, 3) 和 (2, 3, 1, 4) 作为生成元的 交错群 
的凯莱图，它是 截角四面体图 的有向形式。
如果 完全图 
的三个顶点被不同颜色的石头覆盖，并且任何石头都可以移动到空顶点，则所有位置的图形成一个凯莱图，边表示相邻位置（左图）。这对应于 对称群 
的凯莱图，使用元素 (2, 1, 3, 4)、(3, 2, 1, 4) 和 (4, 2, 3, 1) 作为生成元。结果证明，该图是唯一具有 24 个顶点的 立方对称图 的有向版本（右图）。
Royle 构建了顶点数不超过 1000 的所有立方凯莱图，但不包括顶点数为 512 和 768 的图。
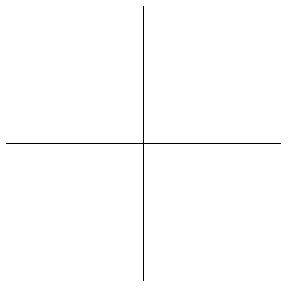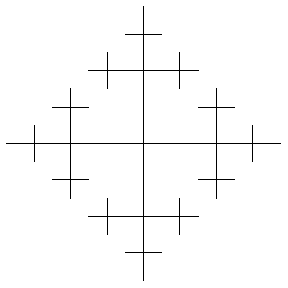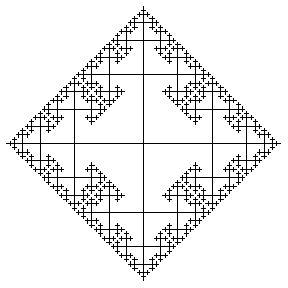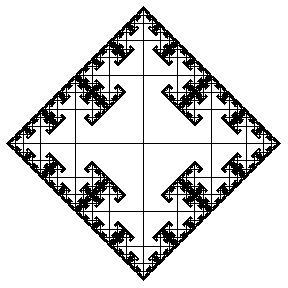
无限群的凯莱图提供了有趣的几何形状。例如，上面说明了两个生成元上的 自由群 的凯莱图（绘制到连续级别），分别表示水平和垂直位移。每个新边都以一半大小绘制，以给出 分形 图像。
