对数

对于以底数 的对数 ，定义为取 底数 的 幂 的反函数，即 。因此，对于任何 和 ,

(1)

或等价地，

(2)

对于任何底数，对数函数在 处有一个奇点。在上图中，蓝色曲线是以 2 为底数的对数 ()，黑色曲线是以 为底数的对数（自然对数 ），红色曲线是以 10 为底数的对数（常用对数，即 ）。

请注意，虽然以 10 为底数的对数在本作品、计算器以及初等代数和微积分教科书中表示为 ，但数学家和高等数学教材一致使用符号 来表示 ，因此使用 来表示常用对数。因此，查阅文献时需要格外小心。

情况更加复杂，因为数论学家（例如，Ivić 2003）通常使用符号 来表示嵌套自然对数 。

在 Wolfram 语言中，以 为底的对数实现为Log[b, x]，而Log[x] 给出自然对数，即，Log[E, x]，其中E是 Wolfram 语言中 e 的符号。

虽然三角函数的幂使用诸如 之类的符号表示，但 较少使用，而更常用符号 。

对数广泛应用于科学和工程的许多领域，在这些领域中，量在很大范围内变化。例如，声音响度的分贝标度、地震震级的里氏震级和恒星亮度的天文标度都是对数标度。

的导数和不定积分由下式给出

			(3)
			(4)

最小值 最大值 实部 虚部

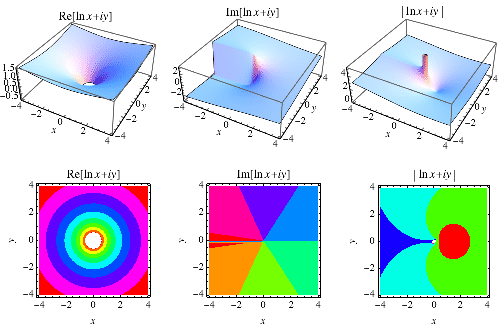对数也可以为复数参数定义，如上所示。如果将对数作为正向函数，则将底数取给定幂的函数称为反对数。

对于 ， 称为特征， 称为尾数。

对数的除法和乘法恒等式可以从恒等式推导出来

(5)

具体而言，对于 ,

			(6)
			(7)
			(8)

有许多性质可用于从一个对数底数更改为另一个对数底数，包括

			(9)
			(10)
			(11)
			(12)
			(13)
			(14)
			(15)
			(16)
			(17)

对数的一个有趣的性质来自于寻找一个数字 ，使得

(18)

(19)

(20)

(21)

因此

(22)

另一个对于任意 成立的相关恒等式由下式给出

(23)

如果 和 是整数，其中一个整数有一个质因数，而另一个整数缺乏该质因数，则 log_ab 形式的数字是无理数。A. Baker 在超越数理论中向前迈进了一大步，证明了 alphalnbeta 形式的数字之和的超越性，其中 和 是代数数。