主题
Search

点阵

DOWNLOAD Mathematica Notebook下载 Wolfram 笔记本
LatticePoints

点阵是规则间隔排列的点阵列。

在平面中，可以构建具有正方形、矩形、六边形等形状的晶胞的点阵。除非另有说明，否则点阵可以指正方形阵列中的点，即坐标为 (m,n,...) 的点，其中 m、 n、... 是 整数。 这种阵列通常被称为 网格 或 网状结构。

点阵通常简称为“格子”，但这不幸地与应用于 格理论 中处理的有序集的同一术语相冲突。每个“点阵”都是在从平面继承的排序下的格，尽管点阵可能不是平面的子格，因为平面中的下确界运算不需要与点阵中的下确界运算一致。另一方面，许多格不是点阵。

格的属性在 Wolfram 语言 中实现为LatticeData[lattice, prop].

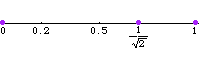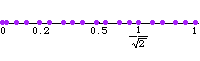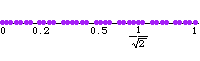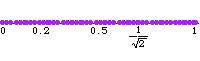
Point lattice

形式上，假设一个格包含原点，则它是 欧几里得空间 的 离散 子群。 也就是说，一个格在加法和逆运算下是封闭的，并且每个点都有一个邻域，其中它是唯一的格点。 常见的例子是 Z subset R 和 Z^2 subset R^2。 通常，格被定义为具有满秩，即 R^n 中的格是 子群

{a_1v_1+...a_nv_n},
(1)

其中 a_i 是整数，v_i 是 线性无关 的向量。 请注意，一个格最多需要 n 个元素来生成它。 例如，子群 {a_1+a_2sqrt(2)} subset R 需要两个生成元，但不是 离散 的，也不是格。 上图说明了由 1 和 1/sqrt(2) 生成的子群不是格，通过显示连续的 a+b/sqrt(2)，其中 b in [0,1]。

从 原点 可见 的格点 比例，如 Castellanos（1988，第 155-156 页）推导的那样，是

(N^'(r))/(N(r))=((24)/(pi^2)r^2+O(rlnr))/(4r^2+O(r))
(2)
=(6/(pi^2)+O((lnr)/r))/(1+O(1/r))
(3)
=6/(pi^2).
(4)

因此，这也是两个随机选择的整数彼此 互质 的概率。

对于 2<=n<=32，可以选择 2n 个格点，其中 x,y in [1,n]，使得没有三个点在一条直 线 上。 对于 n=2，3，... 的不同解（不包括反射和旋转）的数量为 1, 1, 4, 5, 11, 22, 57, 51, 156 ... (OEIS A000769)。 对于大的 n，据推测，最多只能选择 (c+epsilon)n 个格点，且没有三个点 共线，其中

c=(2pi^2/3)^(1/3) approx 1.87
(5)

（Guy 和 Kelly 1968；Guy 1994，第 242 页）。 n^2 个格点 x,y in [1,n] 中，可以选择没有四个点 共圆 的点数为 O(n^(2/3)-epsilon) (Guy 1994，第 241 页)。

PointLatticeParallelograms

在格子上，其中两个对边长度均为 1 的任何 平行四边形 都具有单位面积（Hilbert 和 Cohn-Vossen 1999，第 33-34 页）。

在规则格子上定义的一组特殊的 多边形 是 golygons。 线性变换将格变换为自身的 必要 和 充分 条件是它是 单模 的。 M. Ajtai 已经证明，除非存在用于所有生成向量的有效算法（目前尚不知道），否则没有有效的 算法 可以找到格子中一组生成向量的任何一部分，使其具有最短的长度。 这一结果对密码学和身份验证具有潜在的应用（Cipra 1996）。

另请参阅

Barnes-Wall 格, Blichfeldt 定理, Browkin 定理, 圆格点, Coxeter-Todd 格, Ehrhart 多项式, 椭圆曲线, 高斯圆问题, Golygon, 积分格, Jarnick 不等式, 格路, 格和, Leech 格, 闵可夫斯基凸体定理, 模格, N-簇, Nosarzewska 不等式, Pick 定理, 随机游走, Schinzel 定理, 施罗德数, 环面, 单位格, 可见点, Voronoi 多边形

此条目的部分内容由 Matt Insall 贡献 (作者链接)

此条目的部分内容由 Todd Rowland 贡献

使用 Wolfram|Alpha 探索

参考文献

Apostol, T. 解析数论导论。 纽约：施普林格出版社，1995 年。Castellanos, D. "无处不在的 Pi。" Math. Mag. 61, 67-98, 1988.Cipra, B. "格可能为安全代码奠定更坚实的基础。" Science 273, 1047-1048, 1996.Eppstein, D. "格理论和数的几何。" http://www.ics.uci.edu/~eppstein/junkyard/lattice.html. Gardner, M. "整数格。" 第 21 章，来自科学美国人的数学游戏第六本书。 芝加哥，伊利诺伊州：芝加哥大学出版社，第 208-219 页，1984 年。Guy, R. K. "高斯格点问题"、"具有不同距离的格点"、"圆上没有四个格点" 和 "无三点共线问题"。 §F1、F2、F3 和 F4，数论中未解决的问题，第二版。 纽约：施普林格出版社，第 240-244 页，1994 年。Guy, R. K. 和 Kelly, P. A. "无三点共线问题。" Canad. Math. Bull. 11, 527-531, 1968.Hammer, J. 关于格点的未解决问题。 伦敦：皮特曼，1977 年。Hilbert, D. 和 Cohn-Vossen, S. "点的规则系统。" 第 2 章，几何与想象。 纽约：切尔西，第 32-93 页，1999 年。Knupp, P. 和 Steinberg, S. 网格生成基础。 Boca Raton, FL: CRC Press, 1994 年。Nagell, T. "格点和点阵。" §11，数论导论。 纽约：威利，第 32-34 页，1951 年。Sloane, N. J. A. 序列 A000769/M3252，在 "整数序列在线百科全书" 中。Thompson, J. F.; Soni, B.; 和 Weatherill, N. 网格生成手册。 Boca Raton, FL: CRC Press, 1998 年。

在 Wolfram|Alpha 中被引用

点阵

引用为

Insall, Matt; Rowland, Todd; 和 Weisstein, Eric W. "点阵。" 来自 MathWorld--Wolfram Web 资源。 https://mathworld.net.cn/PointLattice.html

学科分类