主题
Search

割线

DOWNLOAD Mathematica Notebook下载 Wolfram Notebook

割线是在复平面上的一条曲线（端点可以是开的、闭的或半开的），解析多值函数在该曲线上是不连续的。为了方便起见，割线通常被取为直线或线段。割线（即使是由曲线组成的割线）也被称为割线（Arfken 1985, p. 397）、裂缝（Kahan 1987）或分支线。

例如，考虑函数 z^2，它将每个复数 z 映射到一个明确定义的数 z^2。它的反函数 sqrt(z)，另一方面，例如，将值 z=1 映射到 sqrt(1)=+/-1。虽然可以为这些函数选择唯一的主值（在这种情况下，主平方根是正值），但这些选择不能在整个复平面上连续进行。相反，必须出现不连续线。处理这些不连续性的最常见方法是采用所谓的割线。一般来说，割线不是唯一的，而是通过约定选择的，以给出简单的解析性质（Kahan 1987）。有些函数的割线结构相对简单，而另一些函数的割线则极其复杂。

表示多值函数的割线的替代方法是使用黎曼曲面。

除了割线之外，还存在称为分支点的奇点。但是应该注意的是，割线的端点不一定是分支点。

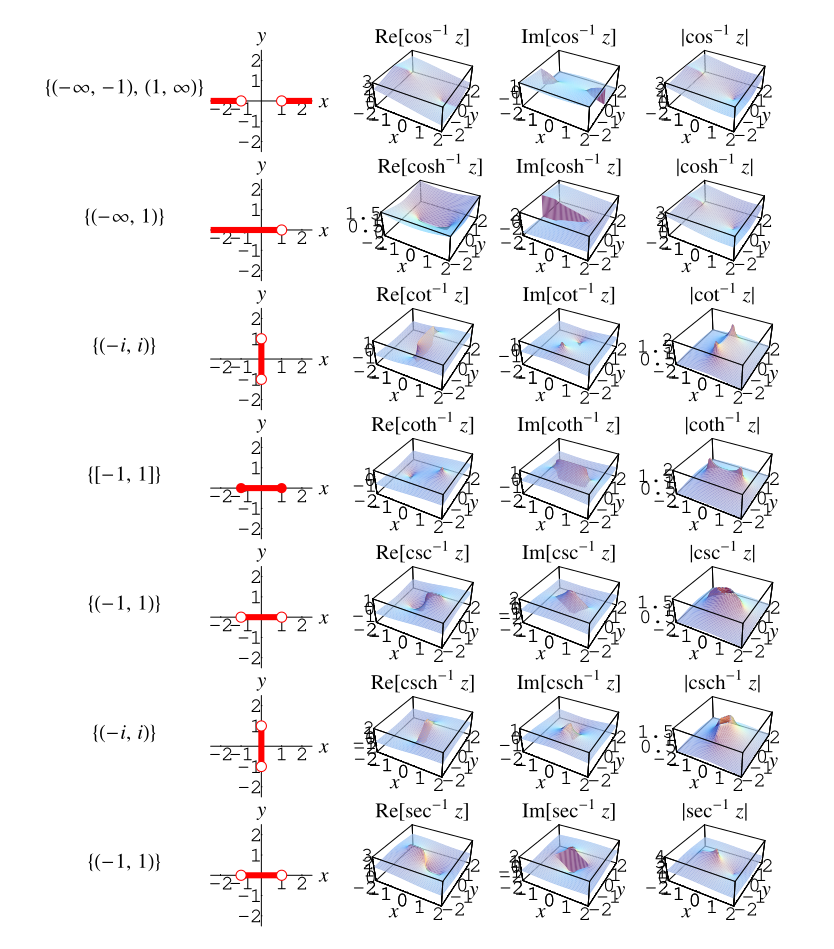
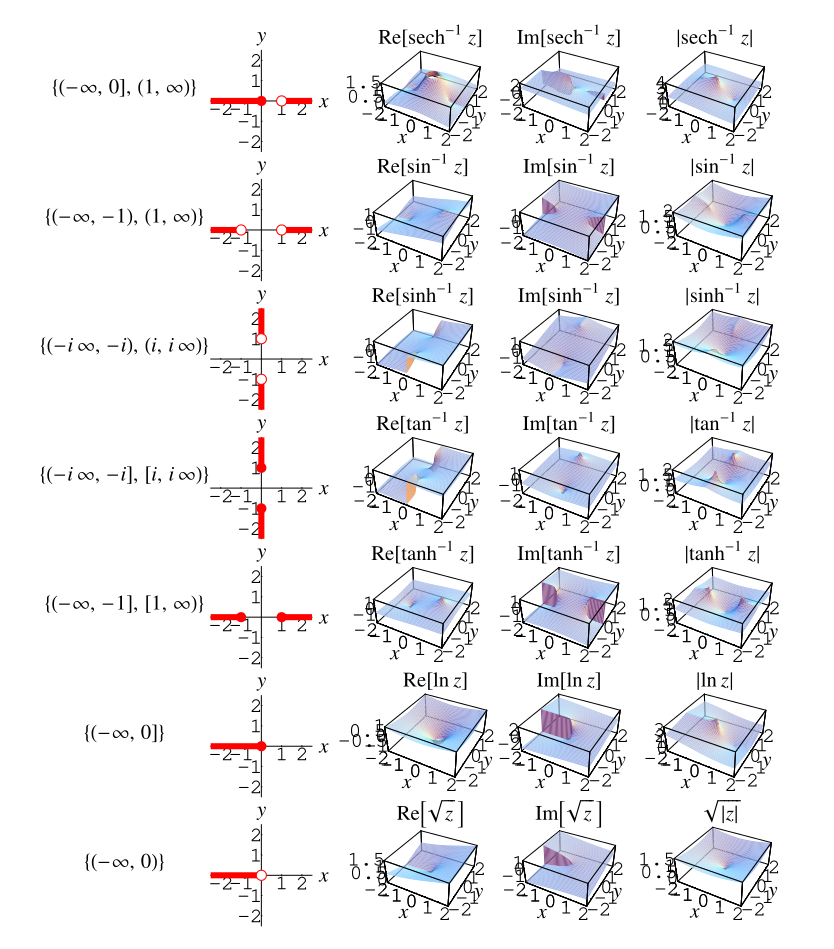
对于单值三角函数、双曲函数、整数幂和指数函数，不会出现割线。然而，它们的多值反函数确实需要割线。下面的图表和表格总结了反三角函数、反双曲函数、非整数幂和对数函数在 Wolfram 语言中采用的割线结构。

BranchCuts1
BranchCuts2
函数名称函数割线
反余割csc^(-1)z(-1,1)
反余弦cos^(-1)z(-infty,-1) 和 (1,infty)
反余切cot^(-1)z(-i,i)
反双曲余割csch^(-1)(-i,i)
反双曲余弦cosh^(-1)(-infty,1)
反双曲余切coth^(-1)[-1,1]
反双曲正割sech^(-1)(-infty,0] 和 (1,infty)
反双曲正弦sinh^(-1)(-iinfty,-i) 和 (i,iinfty)
反双曲正切tanh^(-1)(-infty,-1] 和 [1,infty)
反secantsec^(-1)z(-1,1)
反正弦sin^(-1)z(-infty,-1) 和 (1,infty)
反正切tan^(-1)z(-iinfty,-i] 和 [i,iinfty)
自然对数lnz(-infty,0]
幂z^n,n not in Z(-infty,0) 当 R[n]<=0 时； (-infty,0] 当 R[n]>0 时
平方根sqrt(z)(-infty,0)

另请参阅

分支, 分支点, 割线, 不连续性, 反双曲函数, 反三角函数, 多值函数, 主分支, 主值, 黎曼曲面

使用 探索

参考文献

Abramowitz, M. and Stegun, I. A. (Eds.). Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, 9th printing. New York: Dover, pp. 79 and 86, 1972.Ahlfors, L. V. Complex Analysis, 3rd ed. New York: McGraw-Hill, p. 75, 1979.Arfken, G. Mathematical Methods for Physicists, 3rd ed. Orlando, FL: Academic Press, 1985.Bradford, R.; Corless, R. M.; Davenport, J. H.; Jeffrey, D. J.; and Watt, S. M. "Reasoning About the Elementary Functions of Complex Analysis." Ann. Math. Artificial Intell. 36, 303-318, 2002.Bronshtein, I. N. and Semendyayev, K. A. Handbook of Mathematics, 3rd ed. New York: Springer-Verlag, 1997.Dingle, A. and Fateman, R. J. "Branch Cuts in Computer Algebra." In Symbolic and Algebraic Computation (Ed. J. von zur Gathen and M. Giesbracht). New York: ACM Press, pp. 250-257, 1994.Duffy, D. G. Transform Methods for Solving Partial Differential Equations, 2nd ed. Boca Raton, FL: CRC Press, 2004.Felsen, L. B. and Marcuvitz, I. N. Radiation and Scattering of Waves. New York: IEEE Press, 1994.Kahan, W. "Branch Cuts for Complex Elementary Functions, or Much Ado About Nothing's Sign Bit." In The State of the Art in Numerical Analysis: Proceedings of the Joint IMA/SIAM Conference on the State of the Art in Numerical Analysis Held at the UN (Ed. A. Iserles and M. J. D. Powell). New York: Clarendon Press, pp. 165-211, 1987.Korn, G. A. and Korn, T. M. Mathematical Handbook for Scientists and Engineers. New York: McGraw-Hill, 1968.Mahan, G. D. Applied Mathematics. New York: Kluwer, 2002.Morse, P. M. and Feshbach, H. Methods of Theoretical Physics, Part I. New York: McGraw-Hill, pp. 399-401, 1953.Remmert, R. Funktionentheorie 1. Berlin: Springer-Verlag, 1992.Remmert, R. Funktionentheorie 2. Berlin: Springer-Verlag, 1992.Trott, M. The Mathematica GuideBook for Programming. New York: Springer-Verlag, pp. 188-191, 2004. http://www.mathematicaguidebooks.org/.

在 中被引用

割线

请这样引用

Weisstein, Eric W. "割线。" 来自 Web 资源。 https://mathworld.net.cn/BranchCut.html

主题分类