主题
Search

反三角函数

DOWNLOAD Mathematica Notebook下载 Wolfram 笔记本

反三角函数是多值函数 tan^(-1)z（Zwillinger 1995, p. 465），也表示为 arctanz（Abramowitz 和 Stegun 1972, p. 79; Harris 和 Stocker 1998, p. 311; Jeffrey 2000, p. 124）或 arctgz（Spanier 和 Oldham 1987, p. 333; Gradshteyn 和 Ryzhik 2000, p. 208; Jeffrey 2000, p. 127），即 正切的反函数。变体 Arctanz（例如，Bronshtein 和 Semendyayev, 1997, p. 70）和 Tan^(-1)z 有时用于指代反余切的显式主值，尽管这种区分并不总是被做出（例如，Zwillinger 1995, p. 466）。

ArcTan

反三角函数 tan^(-1)x 在实轴上方的图中绘制。

更糟糕的是，符号 arctanz 有时用于主值，而 Arctanz 用于多值函数（Abramowitz 和 Stegun 1972, p. 80）。请注意，在符号 tan^(-1)z（在北美和全球袖珍计算器中常用）中，tanz 表示正切，而 -1 表示反函数，不是 乘法逆元。

反三角函数的主值实现为ArcTan[z] 在 Wolfram 语言中。在 GNU C 库中，它实现为atan(double x)。

InverseTangentBranchCut

反三角函数是一个多值函数，因此在复平面中需要一个分支切割，Wolfram 语言的约定将其放置在 (-iinfty,-i] 和 [i,iinfty)。这遵循 tan^(-1)z 作为

tan^(-1)z=1/2i[ln(1-iz)-ln(1+iz)].
(1)

在 Wolfram 语言（和这项工作中），此分支切割定义确定了实数 x 的 tan^(-1)x 的范围为 (-pi/2,pi/2)。但是，必须小心，因为其他分支切割定义可能会给出不同的范围（最常见的是，(0,pi)）。

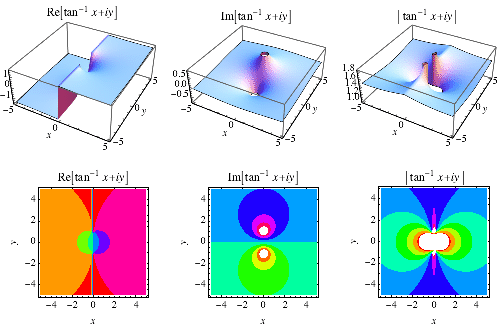ArcTanReImAbs
最小值 最大值
实部
虚部 Powered by webMathematica

反三角函数 tan^(-1)z 在复平面上方的图中绘制。

tan^(-1)z 具有特殊值

tan^(-1)(-infty)=-1/2pi
(2)
tan^(-1)(-i)=-iinfty
(3)
tan^(-1)0=0
(4)
tan^(-1)i=iinfty
(5)
tan^(-1)infty=1/2pi.
(6)

导数 tan^(-1)z 是

d/(dz)tan^(-1)z=1/(1+z^2)
(7)

和不定积分是

inttan^(-1)zdz=ztan^(-1)z-1/2ln(1+z^2)+C.
(8)
InverseTangentYXReIm
InverseTangentYXContours

复数 z=x+iy 的复数辐角通常写为

theta=tan^(-1)(y/x),
(9)

其中 theta，有时也表示为 phi，对应于从正实轴的逆时针角度，即 theta 的值，使得 x=costheta 和 y=sintheta。上面说明了实数值 x 和 y 的 tan^(-1)(y/x) 的图。

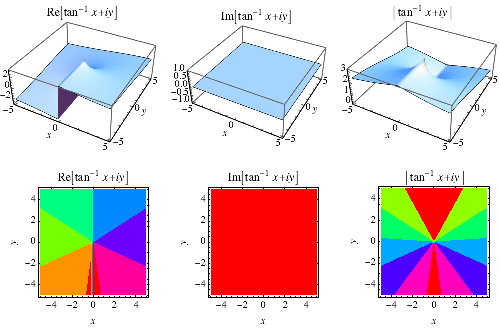InverseTangentReImAbs
最小值 最大值
实部
虚部 Powered by webMathematica

一种特殊的反三角函数，它考虑了 z 所在的象限，并由FORTRAN命令返回ATAN2(y, x)，GNU C 库命令atan2(double y, double x)，以及 Wolfram 语言命令ArcTan[x, y]，并且通常限制在 -pi<theta<=pi 范围内。在退化情况 x=0 时，

phi={-1/2pi if y<0; undefined if y=0; 1/2pi if y>0.
(10)

通常的 tan^(-1)z 具有以下麦克劳林级数：

tan^(-1)z=sum_(n=0)^(infty)((-1)^nz^(2n+1))/(2n+1)
(11)
=z-1/3z^3+1/5z^5-1/7z^7+...
(12)

（OEIS A033999 和 A005408）。欧拉给出的更快速收敛的形式为

tan^(-1)x=sum_(n=0)^infty(2^(2n)(n!)^2)/((2n+1)!)(x^(2n+1))/((1+x^2)^(n+1))
(13)

对于实数 x （Castellanos 1988）。这与欧拉给出的公式有关：

tan^(-1)x=y/x(1+2/3y+(2·4)/(3·5)y^2+(2·4·6)/(3·5·7)y^3+...),
(14)

其中

y=(x^2)/(1+x^2).
(15)

反三角函数公式与许多有趣的 pi 近似值有关

tan^(-1)(1+x)=pi/4+isum_(n=1)^(infty)((-1-i)^n-(i-1)^n)/(2^(n+1)n)x^n
(16)
=1/4pi+1/2x-1/4x^2+1/(12)x^3-1/(40)x^5+1/(48)x^6-1/(112)x^7+...
(17)

（OEIS A075553 和 A075554）。

反三角函数满足

tan^(-1)z=cot^(-1)(1/z)
(18)

对于 z!=0，

tan^(-1)z=-tan^(-1)(-z)
(19)

对于所有复数 z，

tan^(-1)x=1/2pi-cos^(-1)(x/(sqrt(x^2+1)))
(20)
=sin^(-1)(x/(sqrt(x^2+1)))
(21)
=csc^(-1)((sqrt(x^2+1))/x)
(22)

对于所有实数 x，其中最后一个方程的等式被理解为在极限 x->0 下成立，以及

tan^(-1)x={-1/2pi-tan^(-1)(1/x) for x<0; 1/2pi-tan^(-1)(1/x) for x>0
(23)
={-1/2pi+cot^(-1)(-x) for x<0; 1/2pi+cot^(-1)(-x) for x>0
(24)
={-1/2pi-cot^(-1)x for x<0; 1/2pi-cot^(-1)x for x>0
(25)
={-cos^(-1)(1/(sqrt(x^2+1))) for x<0; cos^(-1)(1/(sqrt(x^2+1))) for x>0
(26)
={-sec^(-1)(sqrt(x^2+1)) for x<0; sec^(-1)(sqrt(x^2+1)) for x>0.
(27)

用超几何函数表示，

tan^(-1)z=z_2F_1(1,1/2;3/2;-z^2)
(28)

对于复数 z，以及

tan^(-1)x=x/(1+x^2)_2F_1(1,1;3/2;(x^2)/(1+x^2))
(29)

对于实数 x （Castellanos 1988）。

Castellanos（1986, 1988）还给出了一些关于斐波那契数的奇特公式，

tan^(-1)x=sum_(n=0)^(infty)((-1)^nF_(2n+1)t^(2n+1))/(5^n(2n+1))
(30)
=5sum_(n=0)^(infty)((-1)^nF_(2n+1)^2)/((2n+1)(u+sqrt(u^2+1))^(2n+1))
(31)
=sum_(n=0)^(infty)((-1)^n5^(n+2)F_(2n+1)^3)/((2n+1)(v+sqrt(v^2+5))^(2n+1)),
(32)

其中

t=(2x)/(1+sqrt(1+(4x^2)/5))
(33)
u=5/(4x)(1+sqrt(1+(24)/(25)x^2)),
(34)

和 v 是

8xv^4-100v^3-450xv^2+875v+625x=0.
(35)

的最大正根。反三角函数满足加法公式

tan^(-1)x+tan^(-1)y=tan^(-1)((x+y)/(1-xy))
(36)

对于 -1<x,y<1，以及更复杂的公式

tan^(-1)(1/a)=2tan^(-1)(1/(2a))-tan^(-1)(1/(4a^3+3a))
(37)

对所有复数 a 有效。欧拉已知的另一个恒等式是

tan^(-1)(1/(a-b))=tan^(-1)(1/a)+tan^(-1)(b/(a^2-ab+1))
(38)

对于 (a>b ^ a>0) 或 (a<b ^ a<0)。Lehmer (1938b; Bromwich 1991, Castellanos 1988) 归因于 Charles Dodgson（刘易斯·卡罗尔）的另一个有趣的反三角函数恒等式是

tan^(-1)(p+r)+tan^(-1)(p+q)-tan^(-1)p=1/2pi,
(39)

其中

1+p^2=qr
(40)

和 p,q,r>0。

反三角函数具有连分数表示

tan^(-1)x=x/(1+(x^2)/(3+(4x^2)/(5+(9x^2)/(7+(16x^2)/(9+...)))))
(41)

（Lambert 1770; Lagrange 1776; Wall 1948, p. 343; Olds 1963, p. 138）和

tan^(-1)x=x/(1+(x^2)/(3-x^2+(9x^2)/(5-3x^2+(25x^2)/(7-5x^2+...))))
(42)

由于欧拉，有时被称为欧拉连分数（Borwein et al. 2004, p. 30）。

要数值找到 tan^(-1)x，可以使用以下类似算术-几何平均值的算法。设

a_0=(1+x^2)^(-1/2)
(43)
b_0=1.
(44)

然后计算

a_(i+1)=1/2(a_i+b_i)
(45)
b_(i+1)=sqrt(a_(i+1)b_i),
(46)

反三角函数由下式给出

tan^(-1)x=lim_(n->infty)x/(sqrt(1+x^2)a_n)
(47)

（Acton 1990）。

积分 n 的反三角函数 tan^(-1)n 如果可以表示为形式的有限和，则称为可约的

tan^(-1)n=sum_(k=1)f_ktan^(-1)n_k,
(48)

其中 f_k 是正或负整数，n_i 是整数 <n。tan^(-1)m 是可约的 当且仅当 1+m^2 的所有素因子都出现在 1+n^2 的素因子中，对于 n=1, ..., m-1。第二个必要和充分条件是 1+m^2 的最大素数因子小于 2m。与第二个条件等价的说法是，每个格雷戈里数 t_x=cot^(-1)x 可以唯一地表示为 t_ms 的和，其中 m 是施特默数（Conway 和 Guy 1996）。要找到这种分解，请写出

arg(1+in)=argproduct_(k=1)(1+n_ki)^(f_k),
(49)

因此比率

r=(product_(k=1)(1+n_ki)^(f_k))/(1+in)
(50)

是一个有理数。方程 (50) 也可以写成

r^2(1+n^2)=product_(k=1)(1+n_k^2)^(f_k).
(51)

将 (◇) 写成形式

tan^(-1)n=sum_(k=1)f_ktan^(-1)n_k+ftan^(-1)1
(52)

允许直接转换为相应的反余切公式

cot^(-1)n=sum_(k=1)f_kcot^(-1)n_k+ccot^(-1)1,
(53)

其中

c=2-f-2sum_(k=1)f_r.
(54)

Todd (1949) 给出了 tan^(-1)n 对于 n<=342 的分解表。Conway 和 Guy (1996) 给出了一个类似的关于施特默数的表。

Arndt 和 Gosper 给出了非凡的反三角函数恒等式

sin(sum_(k=1)^(2n+1)tan^(-1)a_k)=((-1)^n)/(2n+1)(sum_(k=1)^(2n+1)product_(j=1)^(2n+1)[a_j-tan((pi(j-k))/(2n+1))])/(sqrt(product_(j=1)^(2n+1)(a_j^2+1))).
(55)

有一组惊人的 BBP 类型公式 用于 tan^(-1)(4/5)

tan^(-1)(4/5)=1/(131072)sum_(k=0)^(infty)1/(1048576^k)[(262144)/(40k+2)-(163840)/(40k+5)-(65536)/(40k+6)+(16384)/(40k+10)-(4096)/(40k+14)-(5120)/(40k+15)+(1024)/(40k+18)-(256)/(40k+22)+(160)/(40k+25)+(64)/(40k+26)-(16)/(40k+30)+4/(40k+34)+5/(40k+35)-1/(40k+38)]
(56)
=1/(131072)sum_(k=0)^(infty)1/(1048576^k)[(393216)/(40k+4)+(163840)/(40k+5)-(131072)/(40k+6)-(163840)/(40k+8)+(24576)/(40k+12)-(8192)/(40k+14)-(15360)/(40k+15)-(10240)/(40k+16)-(1024)/(40k+20)-(512)/(40k+22)-(640)/(40k+24)-(160)/(40k+25)+(96)/(40k+28)-(32)/(40k+30)-(40)/(40k+32)+(15)/(40k+35)+6/(40k+36)-2/(40k+38)]
(57)
=1/(131072)sum_(k=0)^(infty)1/(1048576^k)[(262144)/(40k+1)-(262144)/(40k+3)-(65536)/(40k+5)-(327680)/(40k+6)+(65536)/(40k+7)-(163840)/(40k+8)+(16384)/(40k+9)-(40960)/(40k+10)-(16384)/(40k+11)-(4096)/(40k+13)-(20480)/(40k+14)-(16384)/(40k+15)-(10240)/(40k+16)+(1024)/(40k+17)-(1024)/(40k+19)-(2560)/(40k+20)-(256)/(40k+21)-(1280)/(40k+22)+(256)/(40k+23)-(640)/(40k+24)+(64)/(40k+25)-(64)/(40k+27)-(16)/(40k+29)-(40)/(40k+30)+(16)/(40k+31)-(40)/(40k+32)+4/(40k+33)+(16)/(40k+35)-1/(40k+37)-5/(40k+38)+1/(40k+39)]
(58)
=1/(262144)sum_(k=0)^(infty)1/(1048576^k)[(262144)/(40k+3)+(262144)/(40k+4)+(131072)/(40k+6)-(65536)/(40k+7)+(81920)/(40k+10)+(16384)/(40k+11)+(16384)/(40k+12)+(8192)/(40k+14)-(4096)/(40k+15)+(1024)/(40k+19)+(1024)/(40k+20)+(512)/(40k+22)-(256)/(40k+23)+(64)/(40k+27)+(64)/(40k+28)-(48)/(40k+30)-(16)/(40k+31)+4/(40k+35)+4/(40k+36)+2/(40k+38)-1/(40k+39)],
(59)

找到其中一个是由 Bailey et al. (2006, p. 225) 提出的问题。

另请参阅

欧拉类马钦公式, 高斯类马钦公式, 反余切, 反三角函数, 马钦公式, 类马钦公式, 正切

相关 Wolfram 站点

http://functions.wolfram.com/ElementaryFunctions/ArcTan/

使用 探索

参考文献

Abramowitz, M. 和 Stegun, I. A.(编). "反圆函数." §4.4 在 数学函数手册，包含公式、图表和数学表格，第 9 次印刷。 纽约: Dover, pp. 79-83, 1972.Acton, F. S. "反正切." 在 有效的数值方法，更新和修订版。 华盛顿特区: Math. Assoc. Amer., pp. 6-10, 1990.Apostol, T. M. 微积分，第 2 版，第 1 卷：单变量微积分，线性代数导论。 沃尔瑟姆, 马萨诸塞州: Blaisdell, pp. 255-256, 1967.Arndt, J. "完全无用的公式." http://www.jjj.de/hfloat/hfloatpage.html#formulas.Bailey, D. H.; Borwein, J. M.; Calkin, N. J.; Girgensohn, R.; Luke, D. R.; 和 Moll, V. H. 实验数学行动。 韦尔斯利, 马萨诸塞州: A K Peters, 2007.Beyer, W. H. CRC 标准数学表格，第 28 版。 博卡拉顿, 佛罗里达州: CRC Press, pp. 142-143 和 220, 1987.Borwein, J.; Bailey, D.; 和 Girgensohn, R. "欧拉的连分数." §1.8.2 在 数学实验：发现的计算路径。 韦尔斯利, 马萨诸塞州: A K Peters, p. 30, 2004.Bronshtein, I. N. 和 Semendyayev, K. A. 数学手册，第 3 版。 纽约: Springer-Verlag, p. 70, 1997.Bromwich, T. J. I. 和 MacRobert, T. M. 无限级数理论导论，第 3 版。 纽约: Chelsea, 1991.Castellanos, D. "具有斐波那契系数的快速收敛展开式." Fib. Quart. 24, 70-82, 1986.Castellanos, D. "无处不在的 Pi. 第一部分." Math. Mag. 61, 67-98, 1988.Conway, J. H. 和 Guy, R. K. "施特默数." 数字之书。 纽约: Springer-Verlag, pp. 245-248, 1996.GNU C 库. "数学：反三角函数." https://gnu.ac.cn/manual/glibc-2.2.3/html_chapter/libc_19.html#SEC389.Gosper, R. W. "Joerg Arndt 好心地转发给我." math-fun@cs.arizona.edu 帖子, 1 月 14 日, 1997.Gradshteyn, I. S. 和 Ryzhik, I. M. 积分、级数和乘积表，第 6 版。 圣地亚哥, 加利福尼亚州: Academic Press, 2000.Harris, J. W. 和 Stocker, H. 数学和计算科学手册。 纽约: Springer-Verlag, p. 311, 1998.Hildebrand, J. D. "Arctan() 赞赏主页!" http://www.opensky.ca/~jdhildeb/arctan/.Jeffrey, A. "反三角函数和双曲函数." §2.7 在 数学公式和积分手册，第 2 版。 奥兰多, 佛罗里达州: Academic Press, pp. 124-128, 2000.Lagrange, J.-L. "关于积分计算中连分数的使用." Nouv. mém. de l'académie royale des sciences et belles-lettres Berlin, 236-264, 1776. 重印于 Oeuvres, 第 4 卷, pp. 301-302.Lambert, J. L. 数学及其应用贡献。 第 2 部分。柏林, 1770.Lehmer, D. H. "关于 pi 的反余切关系." Amer. Math. Monthly 45, 657-664, 1938.Olds, C. D. 连分数。 纽约: Random House, 1963.Salamin, G. Beeler, M.; Gosper, R. W.; 和 Schroeppel, R. 中的第 137 项 HAKMEM. 剑桥, 马萨诸塞州: MIT 人工智能实验室, 备忘录 AIM-239, pp. 67-68, 1972 年 2 月. http://www.inwap.com/pdp10/hbaker/hakmem/pi.html#item137.Sloane, N. J. A. 序列 A005408/M2400, A033999, A075553, 和 A075554 在 "整数序列在线百科全书" 中.Spanier, J. 和 Oldham, K. B. "反三角函数." 第 35 章 在 函数图集。 华盛顿特区: Hemisphere, pp. 331-341, 1987.Todd, J. "关于反正切关系的问题." Amer. Math. Monthly 56, 517-528, 1949.Wall, H. S. 连分数解析理论。 纽约: Chelsea, 1948.Zwillinger, D.(编). "反圆函数." §6.3 在 CRC 标准数学表格和公式。 博卡拉顿, 佛罗里达州: CRC Press, pp. 465-467, 1995.

在 上引用

反三角函数

请引用为

Weisstein, Eric W. "反三角函数." 来自 Web 资源. https://mathworld.net.cn/InverseTangent.html

学科分类