主题
Search

反双曲正切

DOWNLOAD Mathematica Notebook下载 Wolfram Notebook
ArcTanh
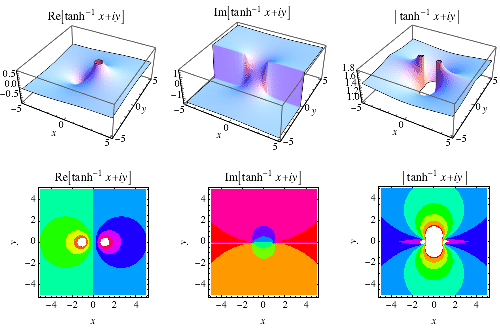
ArcTanhReImAbs
最小值 最大值
实部
虚部 Powered by webMathematica

反双曲正切 tanh^(-1)z (Zwillinger 1995, p. 481; Beyer 1987, p. 181)，有时称为面积双曲正切 (Harris and Stocker 1998, p. 267)，是 多值函数，它是 反函数 双曲正切 的反函数。

该函数有时表示为 arctanhz (Jeffrey 2000, p. 124) 或 Arthz (Gradshteyn and Ryzhik 2000, p. xxx)。 变体 Arctanhz 或 Artanhz (Harris and Stocker 1998, p. 263) 有时用于指代反双曲正切的显式 主值，尽管这种区分并非总是做出。 更糟糕的是，符号 arctanhz 有时用于主值，而 Arctanhz 用于多值函数 (Abramowitz and Stegun 1972, p. 87)。 请注意，在符号 tanh^(-1)z 中，tanhz 是 双曲正切，而上标 -1 表示 反函数，不是乘法逆元。

反双曲正切的 主值 在 Wolfram 语言 中实现为ArcTanh[z]，在 GNU C 库中实现为atanh(double x)。

InverseHyperbolicTangentBranchCut

反双曲正切是 多值函数，因此需要在 复平面 中进行 分支切割，Wolfram 语言 的约定将其放置在线段 (-infty,-1] 和 [1,infty) 处。 这遵循 tanh^(-1)z 的定义，即

tanh^(-1)z=1/2[ln(1+z)-ln(1-z)].
(1)

反双曲正切用 反正切 表示为

tanh^(-1)z=1/itan^(-1)(iz)
(2)

(Gradshteyn 和 Ryzhik 2000, p. xxx)。 对于实数 x<1，这简化为

tanh^(-1)x=1/2ln((1+x)/(1-x)).
(3)

反双曲正切的 导数 为

d/(dz)tanh^(-1)z=1/(1-z^2),
(4)

而 不定积分 为

inttanh^(-1)zdz=ztanh^(-1)z+1/2ln(z^2-1)+C.
(5)

它具有特殊值

tanh^(-1)0=0
(6)
tanh^(-1)1=infty
(7)
tanh^(-1)infty=-1/2pii
(8)
tanh^(-1)i=1/4pii.
(9)

它具有麦克劳林级数

tanh^(-1)z=sum_(n=1)^(infty)(z^(2n-1))/(2n-1)
(10)
=z+1/3z^3+1/5z^5+1/7z^7+1/9z^9+...
(11)
tanh^(-1)z=-1/2pii+sum_(n=1)^(infty)(z^(-2n+1))/(2n-1)
(12)
=-1/2pii+z+1/3z^3+1/5z^5+1/7z^7+...
(13)

(OEIS A005408)。

涉及 tanh^(-1)z 的 不定积分 由下式给出

int(dx)/(xsqrt(a+bx))=ln[(sqrt(a+bx)-sqrt(a))/(sqrt(a+bx)+sqrt(a))]
(14)
=ln[((sqrt(a+bx)-sqrt(a))^2)/((a+bx)-a)]
(15)
=ln[((2a+bx)-2sqrt(a(a+bx)))/(bx)]
(16)
=2tanh^(-1)(-sqrt(a/(a+bx)))
(17)

当 a>0 时。

另请参阅

双曲正切, 反双曲余切, 反双曲函数

相关的 Wolfram 网站

http://functions.wolfram.com/ElementaryFunctions/ArcTanh/

使用 Wolfram|Alpha 探索

参考文献

Abramowitz, M. 和 Stegun, I. A. (编)。 "反双曲函数。" 《数学函数手册，包含公式、图表和数学表格》，第 9 版，§4.6。 纽约：Dover，pp. 86-89，1972。Beyer, W. H. CRC 标准数学表格，第 28 版。 Boca Raton, FL: CRC Press, pp. 142-143，1987。GNU C Library. "数学：反三角函数。" https://gnu.ac.cn/manual/glibc-2.2.3/html_chapter/libc_19.html#SEC391。Gradshteyn, I. S. 和 Ryzhik, I. M. 积分表、级数表和乘积表，第 6 版。 San Diego, CA: Academic Press, p. xxx，2000。Harris, J. W. 和 Stocker, H. 数学和计算科学手册。 纽约：Springer-Verlag，1998。Jeffrey, A. "反三角函数和双曲函数。" 《数学公式和积分手册》，第 2 版，§2.7。 Orlando, FL: Academic Press, pp. 124-128，2000。Sloane, N. J. A. 序列 A005408/M2400，收录于“整数序列在线百科全书”。Spanier, J. 和 Oldham, K. B. "反三角函数。" 《函数图集》，第 35 章。 Washington, DC: Hemisphere，pp. 331-341，1987。Zwillinger, D. (编)。 "反双曲函数。" 《CRC 标准数学表格和公式》，§6.8。 Boca Raton, FL: CRC Press, pp. 481-483，1995。

在 Wolfram|Alpha 中引用

反双曲正切

请引用为

Weisstein, Eric W. "反双曲正切。" 来自 MathWorld--Wolfram Web 资源。 https://mathworld.net.cn/InverseHyperbolicTangent.html

主题分类