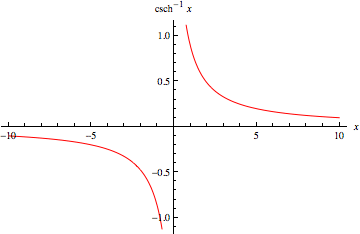主题
Search

反双曲余割

DOWNLOAD Mathematica Notebook下载 Wolfram 笔记本
ArcCschReal
最小值 最大值
Powered by webMathematica
ArcCschReImAbs
最小值 最大值
实部
虚部 Powered by webMathematica

反双曲余割 csch^(-1)z (Zwillinger 1995, p. 481)，有时称为面积双曲余割 (Harris and Stocker 1998, p. 271)，有时记为 cosech^(-1)z (Beyer 1987, p. 181) 或 arccschz (Abramowitz and Stegun 1972, p. 87; Jeffrey 2000, p. 124)，是 多值函数，它是 反函数 双曲余割 的反函数。变体 Arccschz (Abramowitz and Stegun 1972, p. 87) 和 Arcschz (Harris and Stocker 1998, p. 263) 有时用于指代显式的 主值。更糟糕的是，符号 arccschz 有时用于主值，而 Arccschz 则用于多值函数 (Abramowitz and Stegun 1972, p. 87)。请注意，在符号 csch^(-1)z 中，cschz 是 双曲余割，而上标 -1 表示 反函数，不是 乘法逆元。

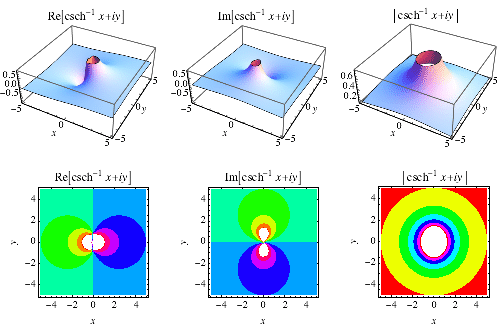
反双曲余割是一个 多值函数，因此在 复平面 中需要一个 分支切割，Wolfram Language 的约定将其放置在 (-i,i)。

主值 csch^(-1)z 在 Wolfram Language 中实现为ArcCsch[z]。

它具有特殊值

csch^(-1)2=lnphi,
(1)

其中 phi 是 黄金比例。

InverseHyperbolicCosecantBranchCut

反双曲余割是一个 多值函数，因此在 复平面 中需要一个 分支切割，Wolfram Language 的约定将其放置在线段 (-i,i) 上。这遵循 csch^(-1)z 的定义，即

csch^(-1)z=ln(sqrt(1+1/(z^2))+1/z).
(2)

反双曲余割的 导数 是

d/(dz)csch^(-1)z=-1/(z^2sqrt(1+1/(z^2))),
(3)

而 不定积分 是

intcsch^(-1)zdz =zcsch^(-1)z+ln[z(1+sqrt((1+z^2)/(z^2)))]+C.
(4)

对于实数 x，它满足

csch^(-1)x={ln((1-sqrt(1+x^2))/x) for x<0; ln((1+sqrt(1+x^2))/x) for x>0.
(5)

反双曲余割具有关于 0 的 Puiseux 级数

csch^(-1)x=-lnx+ln2+sum_(n=1)^(infty)((-1)^(n+1)(2n-1)!!)/(2n(2n)!!)x^(2n)
(6)
=-lnx+ln2+1/4x^2-3/(32)x^4+5/(96)x^6+...
(7)

(OEIS A052468 和 A052469) 以及关于 infty 的 泰勒级数，为

csch^(-1)x=sum_(k=1)^(infty)(P_(k-1)(0))/kx^(-k)
(8)
=sum_(n=1)^(infty)((-1)^n(1/2)_(n-1))/((2n-1)(n-1)!)x^(1-2n)
(9)
=x^(-1)-1/6x^(-3)+3/(40)x^(-5)-5/(112)x^(-7)+...
(10)

(OEIS A055786 和 A002595)，其中 P_k(x) 是 勒让德多项式，(1/2)_n 是 波赫哈默尔符号。

另请参见

双曲余割, 反双曲函数

相关 Wolfram 网站

http://functions.wolfram.com/ElementaryFunctions/ArcCsch/

在 Wolfram|Alpha 中探索

参考文献

Abramowitz, M. and Stegun, I. A. (Eds.). "Inverse Hyperbolic Functions." §4.6 in Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, 9th printing. New York: Dover, pp. 86-89, 1972.Beyer, W. H. CRC Standard Mathematical Tables, 28th ed. Boca Raton, FL: CRC Press, pp. 142-143, 1987.Harris, J. W. and Stocker, H. Handbook of Mathematics and Computational Science. New York: Springer-Verlag, 1998.Jeffrey, A. "Inverse Trigonometric and Hyperbolic Functions." §2.7 in Handbook of Mathematical Formulas and Integrals, 2nd ed. Orlando, FL: Academic Press, pp. 124-128, 2000.Sloane, N. J. A. Sequences A052468, A052469, A055786 and A002595/M4233 in "The On-Line Encyclopedia of Integer Sequences."Spanier, J. and Oldham, K. B. "Inverse Trigonometric Functions." Ch. 35 in An Atlas of Functions. Washington, DC: Hemisphere, pp. 331-341, 1987.Zwillinger, D. (Ed.). "Inverse Hyperbolic Functions." §6.8 in CRC Standard Mathematical Tables and Formulae. Boca Raton, FL: CRC Press, pp. 481-483, 1995.

在 Wolfram|Alpha 上引用

反双曲余割

请引用为

Weisstein, Eric W. "反双曲余割。" 来自 MathWorld--Wolfram Web 资源。 https://mathworld.net.cn/InverseHyperbolicCosecant.html

主题分类