复数辐角

最小值 最大值 实部 虚部

一个复数 可以表示为

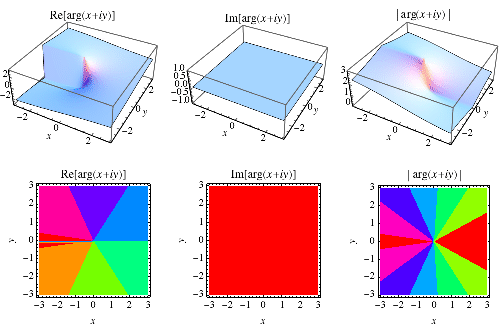
(1)

其中 是一个正实数，称为 的复数模量，而 (有时也表示为 ) 是一个实数，称为辐角。辐角有时也称为相位，或者更少见且更令人困惑地称为幅度 (Derbyshire 2004, pp. 180-181 and 376)。

数字 的复数辐角在 Wolfram 语言中实现为Arg[z].

复数辐角可以计算为

(2)

这里，，有时也表示为 ，对应于从正 实轴逆时针方向的角度，即 的值，使得 且 。此处使用的特殊类型的反正切考虑了 所在的象限，并由FORTRAN命令ATAN2(y, x)和 Wolfram 语言函数返回ArcTan[x, y]，并且通常（包括通过 Wolfram 语言 函数Arg）限制在范围 内。在 的退化情况下，

(3)

复数辐角的特殊值包括

			(4)
			(5)
			(6)
			(7)
			(8)

根据辐角的定义，两个数字乘积的复数辐角等于它们辐角的和，

			(9)
			(10)
			(11)
			(12)

因此得出

(13)

给出特殊情况

(14)

请注意，如果辐角被限制在 ，则所有这些恒等式仅在模 的因子下成立。