双曲线

双曲线（复数形式为“hyperbolas”；Gray 1997, p. 45）是一个 圆锥截面，定义为所有点 在 平面 内的 轨迹，这些点到两个固定点（焦点 和 ）的距离 和 之差的绝对值，这两个固定点相距 ，是一个给定的 正 常数 ,

（Hilbert 和 Cohn-Vossen 1999, p. 3）。令点 落在左侧 -截距上，则要求

因此常数由 给出，即 -截距之间的距离（上图左侧）。双曲线具有一个重要的性质：从一个 焦点 发出的光线，以某种方式反射，使得出射路径沿着从另一个 焦点 穿过交点的直线（上图右侧）。

等轴双曲线 的特殊情况，对应于离心率 的双曲线，最早由 Menaechmus 研究。欧几里得和阿里斯泰俄斯写了关于一般双曲线的文章，但只研究了它的一支。双曲线的现名由阿波罗尼奥斯给出，他是第一个研究双曲线两支的人。焦点 和 圆锥曲线准线 由帕普斯考虑（MacTutor 档案馆）。双曲线是逃逸轨迹上物体的轨道形状（即具有正能量的物体），例如一些彗星，围绕一个固定质量的物体，例如太阳。

双曲线可以通过连接刚性杆 的自由端 来构造，其中 是一个 焦点，另一个 焦点 用绳子 连接。当杆 绕 旋转，并且 保持紧贴杆（即位于杆上）时， 的 轨迹 是双曲线的一个分支（上图左侧；Wells 1991）。阿波罗尼奥斯定理指出，对于在点 与双曲线相切，并在点 和 与渐近线 相交 的线段，则 是常数，且 （上图右侧；Wells 1991）。

设双曲线上的点 的笛卡尔坐标为 ，则双曲线的定义 给出

重新排列并完成平方项得到

两边同时除以 得到

与 椭圆 的定义类比，定义

因此，半长轴 平行于 x 轴，半短轴 平行于 y 轴 的双曲线方程由下式给出：

或者，对于中心在点 而不是 的情况，方程为：

与 椭圆 不同，双曲线没有点实际位于 半短轴 上，而是比率 决定了双曲线的垂直缩放。离心率 （总是满足 ）定义为：

在双曲线的标准方程中，中心位于 ，焦点 位于 ，顶点位于 。所谓的 渐近线 （在上图中以虚线显示）可以通过将通用方程 (8) 右侧的 1 替换为 0 找到：

因此，斜率 为 。

的特殊情况（上图左侧）被称为 等轴双曲线，因为 渐近线 是 互相垂直 的。

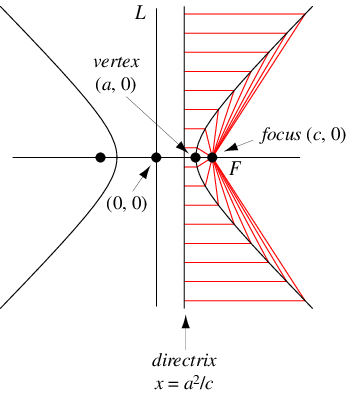
双曲线也可以定义为点的 轨迹，这些点到 焦点 的距离与到垂直线 （称为 圆锥曲线准线）的水平距离成比例，其中比例 。设 为比例， 为准线到中心的距离，则

其中 因此仅仅是 离心率 。

像非圆形 椭圆 一样，双曲线有两个不同的 焦点 和两个相关的 圆锥曲线准线，每个 圆锥曲线准线 都 垂直于 连接两个焦点的直线 (Eves 1965, p. 275)。

双曲线的 焦参数 为

在 极坐标 中，中心位于 原点 的双曲线方程（即 ）为

在以 焦点 为中心的 极坐标 中，

如上图所示。

以 焦点 为原点的双中心 双极坐标 方程为

双曲线右支的 参数方程 由下式给出：

其中 是 双曲余弦， 是 双曲正弦，它们覆盖了双曲线的右支。

覆盖双曲线两个分支的参数表示为

其中 ，在 处不连续。上述参数化的 弧长、曲率 和 切线角 为

其中 是 第二类椭圆积分。

双曲线的 特殊仿射曲率 为

包含固定在三维空间中的 椭圆 的可变 圆锥 的顶点的 轨迹 是通过 椭圆 的 焦点 的双曲线。此外，包含该双曲线的 圆锥 的顶点的 轨迹 是原始 椭圆。此外，椭圆 和双曲线的 离心率 互为倒数。