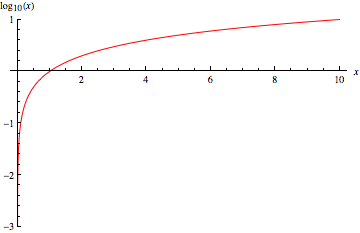
 |
常用对数是以 10 为 底数 的 对数。物理学家、工程师和计算器键盘使用符号 
来表示常用对数。然而，数学家通常使用相同的符号来表示 自然对数 ln，
。更糟糕的是，在俄罗斯文献中，符号 
用于表示以 10 为底的对数，这与符号 lg 用于表示以 2 为底的对数相冲突。为了避免所有歧义，最好明确指定 
以表示以 10 为底的对数。在本文中，
, 
用于表示 自然对数，而 
用于表示以 底数 2 为底的对数。
情况甚至更加复杂，因为数论学家（例如，Ivić 2003）通常使用符号 
来表示 嵌套自然对数 
。
常用对数在 Wolfram 语言 中实现为Log[10, x] 和Log10[x]。
Hardy 和 Wright (1979, p. 8) 断言常用对数“没有数学意义”。
常用对数和自然对数可以用彼此表示为
 |
和
 |
 |
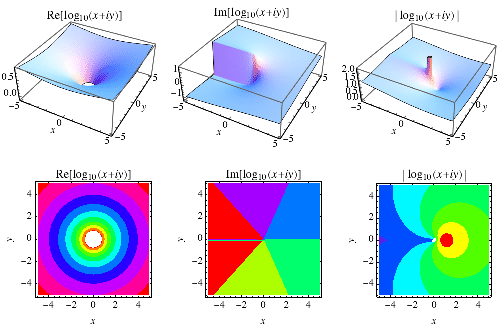扩展到 复平面 的常用对数如上图所示。
的最大素因子的一个问题。” 2003 年 11 月 5 日。