双曲直角

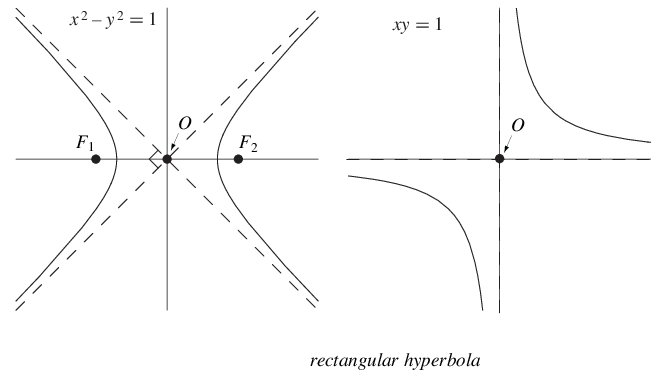
一种双曲线，其渐近线是垂直的，也称为等边双曲线或直角双曲线。当半长轴和半短轴相等时，就会发生这种情况。这对应于取，得到离心率。将代入双曲线的一般方程，其中半长轴平行于x轴，半短轴平行于y轴（即，垂直圆锥曲线准线），

(1)

因此得到

(2)

向左和向右开口的双曲直角具有极坐标方程

(3)

并且在第一象限和第三象限开口的双曲直角具有笛卡尔方程

(4)

双曲直角右分支的参数方程由下式给出

			(5)
			(6)

其中是双曲余弦，是双曲正弦。对于上述参数化，当时，曲率、弧长和切线角为

			(7)
			(8)
			(9)
			(10)
			(11)

其中是第二类椭圆积分，是伽马函数，是超几何函数，是不完全贝塔函数，是双曲正切。

给出两个分支的参数化由下式给出

			(12)
			(13)

其中，并且在处不连续。

中心位于双曲线中心的反演中心的双曲直角的反曲线是伯努利双纽线 (Wells 1991)。

如果三角形的三个顶点位于双曲直角上，那么垂心也位于其上 (Wells 1991)。等效地，如果四个点形成一个垂心系统，那么存在一个通过这些点的双曲直角族。此外，这些双曲线的中心的轨迹是三角形的九点圆 (Wells 1991)。

如果四个点不形成垂心系统，那么存在一个唯一的通过它们的双曲直角，并且其中心由每次取三个点的点的九点圆的交点给出 (Wells 1991)。