主题
Search

抛物线

下载 Mathematica 笔记本下载 Wolfram 笔记本
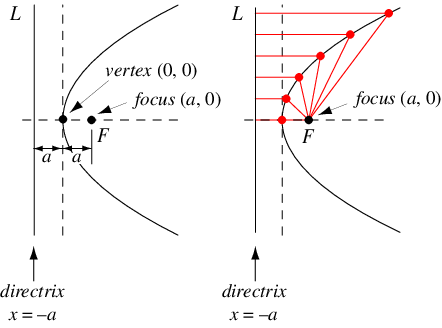
ParabolaDirectrix

抛物线（复数形式为“抛物线”；Gray 1997，第 45 页）是在平面内所有点组成的集合，这些点到给定直线 L ( 圆锥曲线准线 ) 和给定点 F （不在直线上的焦点）的距离相等。焦参数（即准线和焦点之间的距离）因此由 p=2a 给出，其中 a 是从顶点到准线或焦点的距离。通过围绕对称轴旋转抛物线获得的旋转曲面称为抛物面。

ParabolaFocus

梅内克缪斯研究了抛物线，试图实现倍立方。梅内克缪斯通过找到两个抛物线 x^2=y 和 y^2=2x 的交点解决了这个问题。欧几里得写了关于抛物线的文章，阿波罗尼奥斯给它起了现在的名字。帕斯卡将抛物线视为圆的投影，伽利略表明在均匀重力下，抛射体的轨迹是抛物线。格雷戈里和牛顿考虑了抛物线的折射线性质，即把平行光线汇聚到一个焦点上（MacTutor 档案馆），如上图所示。

对于顶点在 (0, 0) 且开口向右的抛物线，笛卡尔坐标系中的方程为

sqrt((x-a)^2+y^2)=x+a
(1)
(x-a)^2+y^2=(x+a)^2
(2)
x^2-2ax+a^2+y^2=x^2+2ax+a^2
(3)
y^2=4ax.
(4)

量 4a 被称为焦弦。

如果顶点在 (x_0,y_0) 而不是 (0, 0)，则焦弦为 a 的抛物线方程为

(y-y_0)^2=4a(x-x_0).
(5)

顶点在 (x_0,y_0) 且焦弦为 a 的开口向上的抛物线方程为

(x-x_0)^2=4a(y-y_0).
(6)
Parabola3Points

三个点唯一确定一个准线平行于 x 轴的抛物线和一个准线平行于 y 轴的抛物线。如果这些抛物线通过三个点 (x_1,y_1)、(x_2,y_2) 和 (x_3,y_3)，则它们的方程由下式给出

|x^2 x y 1; x_1^2 x_1 y_1 1; x_2^2 x_2 y_2 1; x_3^2 x_3 y_3 1|=0
(7)

和

|y^2 x y 1; y_1^2 x_1 y_1 1; y_2^2 x_2 y_2 1; y_3^2 x_3 y_3 1|=0.
(8)
ParabolaPolar

在极坐标系中，参数为 a 且中心为 (0, 0) 的抛物线方程由下式给出

r=-(2a)/(1+costheta)
(9)

（左图）。通过建立坐标系 (x^',y^')=(x-a,y) 并代入 r=sqrt(x^('2)+y^('2)) 和 theta=tan^(-1)(y^'/x^') 可以看出与笛卡尔形式的等价性，得到

sqrt((x-a)^2+y^2)=-(2a)/(1+(x-a)/(sqrt((x-a)^2+y^2))).
(10)

展开并收集项，

a+x+sqrt((a-x)^2+y^2)=0,
(11)

因此求解 y^2 得到 (◇)。一组共焦抛物线显示在右图中。

在垂足坐标系中，垂足点位于焦点时，方程为

p^2=ar.
(12)

抛物线可以参数化地写成

x=at^2
(13)
y=2at
(14)

或

x=(t^2)/(4a)
(15)
y=t.
(16)

抛物线段是李萨如图形。

ParabolaEnvelope

抛物线可以通过连接两条线段上的相对点来生成为两条相交线段的包络线（Wells 1991）。

ParabolaTangents

在上图中，直线 SPA、SQB 和 POQ 分别在点 A、B 和 O 处与抛物线相切。然后 SP/PA=QO/OP=BQ/QS (Wells 1991)。此外，DeltaPQS 的外接圆通过焦点 F (Honsberger 1995，第 47 页)。此外，从焦点到抛物线切线的垂足始终位于顶点处的切线上（Honsberger 1995，第 48 页）。

ParabolaTangentLines

给定一个位于抛物线“外部”的任意点 P，可以通过绘制以 PF 为直径的圆来构造通过 P 的抛物线切线或切线，其中 F 是焦点。然后找到圆与通过 V 的垂直切线相交的点 A 和 B。点 T_A 和 T_B （在退化情况下可以坍缩为单点）然后是直线 PA 和 PB 与抛物线的切点 (Wells 1991)。

曲率、弧长和切线角为

kappa(t)=1/(2a(1+t^2)^(3/2))
(17)
s(t)=a(tsqrt(1+t^2)+sinh^(-1)t)
(18)
phi(t)=tan^(-1)t.
(19)

抛物线的切向量为

x_T(t)=1/(sqrt(1+t^2))
(20)
y_T(t)=t/(sqrt(1+t^2)).
(21)

下图显示了抛物线的法向量和切向量。

ParabolaNormalTangent

另请参见

圆锥曲线、椭圆、双曲线、抛物线折射线、抛物线渐屈线、抛物线反演曲线、抛物线渐伸线、抛物线负垂足曲线、抛物线垂足曲线、抛物面、二次曲线、反射性质、契尔恩豪森三次垂足曲线、韦尔奇窗函数 在 MathWorld 课堂中探索此主题

使用 Wolfram|Alpha 探索

参考文献

Beyer, W. H. CRC Standard Mathematical Tables, 28th ed. Boca Raton, FL: CRC Press, pp. 198 and 222-223, 1987.Casey, J. "The Parabola." Ch. 5 in A Treatise on the Analytical Geometry of the Point, Line, Circle, and Conic Sections, Containing an Account of Its Most Recent Extensions, with Numerous Examples, 2nd ed., rev. enl. Dublin: Hodges, Figgis, & Co., pp. 173-200, 1893.Coxeter, H. S. M. "Conics." §8.4 in Introduction to Geometry, 2nd ed. New York: Wiley, pp. 115-119, 1969.Gray, A. Modern Differential Geometry of Curves and Surfaces with Mathematica, 2nd ed. Boca Raton, FL: CRC Press, 1997.Hilbert, D. and Cohn-Vossen, S. Geometry and the Imagination. New York: Chelsea, p. 4, 1999.Honsberger, R. Episodes in Nineteenth and Twentieth Century Euclidean Geometry. Washington, DC: Math. Assoc. Amer., pp. 47-48, 1995.Lawrence, J. D. A Catalog of Special Plane Curves. New York: Dover, pp. 67-72, 1972.Lockwood, E. H. "The Parabola." Ch. 1 in A Book of Curves. Cambridge, England: Cambridge University Press, pp. 2-12, 1967.Loomis, E. S. "The Parabola." §2.5 in The Pythagorean Proposition: Its Demonstrations Analyzed and Classified and Bibliography of Sources for Data of the Four Kinds of "Proofs," 2nd ed. Reston, VA: National Council of Teachers of Mathematics, pp. 25-28, 1968.MacTutor History of Mathematics Archive. "Parabola." http://www-groups.dcs.st-and.ac.uk/~history/Curves/Parabola.html.Pappas, T. "The Parabolic Ceiling of the Capitol." The Joy of Mathematics. San Carlos, CA: Wide World Publ./Tetra, pp. 22-23, 1989.Wells, D. The Penguin Dictionary of Curious and Interesting Geometry. London: Penguin, pp. 169-172, 1991.Yates, R. C. "Conics." A Handbook on Curves and Their Properties. Ann Arbor, MI: J. W. Edwards, pp. 36-56, 1952.

请引用为

Weisstein, Eric W. "抛物线。" 来源：MathWorld--Wolfram Web 资源。 https://mathworld.net.cn/Parabola.html

主题分类