主题
Search

椭圆

下载 Mathematica Notebook下载 Wolfram Notebook
EllipseBipolar
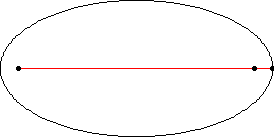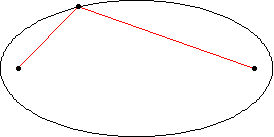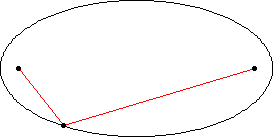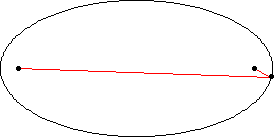
Ellipse construction

椭圆是一条曲线，它是轨迹，由平面内所有点组成，这些点到两个固定点 F_1 和 F_2 （焦点）的距离 r_1 和 r_2 之和为一个给定的正常数 2a （Hilbert 和 Cohn-Vossen 1999, p. 2）。这导致双中心双极坐标方程

r_1+r_2=2a,
(1)

其中 a 是半长轴，坐标系的原点位于其中一个焦点。相应的参数 b 被称为半短轴。

椭圆是圆锥曲线和利萨如曲线。

可以使用Wolfram 语言指定椭圆，使用Circle[{x, y}, {a, b}].

如果线段的端点沿着两条相交线移动，则线段上（或延长线上）的固定点会描绘出椭圆的弧。这被称为椭圆的椭圆规作图法（Eves 1965, p. 177）。

Elliptic gears

可以构造椭圆齿轮，使其彼此平稳旋转（Brown 1871, pp. 14-15; Reuleaux 和 Kennedy 1876, p. 70; Clark 和 Downward 1930; KMODDL）。

椭圆最早由 Menaechmus 研究，由欧几里得研究，并由阿波罗尼奥斯命名。焦点和椭圆的圆锥曲线准线由帕普斯考虑。1602 年，开普勒认为火星的轨道是卵形的；他后来发现它是一个椭圆，太阳位于一个焦点上。事实上，开普勒引入了“焦点”一词，并在 1609 年发表了他的发现。1705 年，哈雷表明，现在以他的名字命名的彗星以椭圆轨道绕太阳运行（MacTutor Archive）。椭圆绕其短轴旋转产生扁球体，而椭圆绕其长轴旋转产生长球体。

穿过焦点的光线在单次反射后将穿过另一个焦点（Hilbert 和 Cohn-Vossen 1999, p. 3）。不穿过焦点的反射将与共焦双曲线或椭圆相切，具体取决于光线是否穿过焦点之间。

让椭圆沿 x 轴延伸，并找到图形的方程 (1)，其中 F_1 和 F_2 位于 (-c,0) 和 (c,0)。在笛卡尔坐标系中，

sqrt((x+c)^2+y^2)+sqrt((x-c)^2+y^2)=2a.
(2)

sqrt((x+c)^2+y^2)+sqrt((x-c)^2+y^2)=2a

(x+c)^2+y^2=4a^2-4asqrt((x-c)^2+y^2)+(x-c)^2+y^2.
(3)

将第二项移到右侧并平方两侧，

sqrt((x-c)^2+y^2)=-1/(4a)(x^2+2xc+c^2+y^2-4a^2-x^2+2xc-c^2-y^2)
(4)
=-1/(4a)(4xc-4a^2)
(5)
=a-c/ax.
(6)

(x+c)^2+y^2=(2a-sqrt((x-c)^2+y^2))^2

x^2-2xc+c^2+y^2=a^2-2cx+(c^2)/(a^2)x^2.
(7)

现在求解平方根项并简化

x^2(a^2-c^2)/(a^2)+y^2=a^2-c^2,
(8)

sqrt((x-c)^2+y^2)=a-(cx)/a

(x^2)/(a^2)+(y^2)/(a^2-c^2)=1.
(9)

最后平方一次以消除剩余的平方根，

b^2=a^2-c^2
(10)

(x-c)^2+y^2=(a-(cx)/a)^2

(x^2)/(a^2)+(y^2)/(b^2)=1.
(11)

将 x 项分组，然后得到

如果椭圆的中心不是位于 (0, 0)，而是位于 (x_0, y_0)，则方程 (◇) 变为

((x-x_0)^2)/(a^2)+((y-y_0)^2)/(b^2)=1.
(12)

((x-x_0)^2)/(a^2)+((y-y_0)^2)/(b^2)=1

x=acost
(13)
y=bsint.
(14)

从椭圆的笛卡尔方程可以看出，该曲线也可以用一个简单的参数形式给出，类似于圆的参数形式，但 x 和 y 坐标具有不同的缩放比例，

ax^2+2bxy+cy^2+2dx+2fy+g=0
(15)

x=acost

Delta=|a b d; b c f; d f g|
(16)
J=|a b; b c|
(17)
I=a+c,
(18)

y=bsint

x_0=(cd-bf)/(b^2-ac)
(19)
y_0=(af-bd)/(b^2-ac),
(20)

一般的二次曲线

a^'=sqrt((2(af^2+cd^2+gb^2-2bdf-acg))/((b^2-ac)[sqrt((a-c)^2+4b^2)-(a+c)]))
(21)
b^'=sqrt((2(af^2+cd^2+gb^2-2bdf-acg))/((b^2-ac)[-sqrt((a-c)^2+4b^2)-(a+c)])).
(22)

Ax^2+Bxy+Cy^2+Dx+Ey+F=0

phi={0 for b=0 and a<c; 1/2pi for b=0 and a>c; 1/2cot^(-1)((a-c)/(2b)) for b!=0 and a<c; pi/2+1/2cot^(-1)((a-c)/(2b)) for b!=0 and a>c.
(23)
EllipseDirectrix

当在定义之后是椭圆

r=(a-c)/(d-a)=(sqrt(b^2+c^2))/d.
(24)

Delta=|(A,B/2,D/2),(B/2,C,E/2),(D/2,E/2,F)|

d=(a^2)/(sqrt(a^2-b^2))=(a^2)/c
(25)
r=(sqrt(a^2-b^2))/a=c/a.
(26)

Delta!=0, J>0, 和 Delta/I<0。还假设椭圆是非退化的（即，它不是一个圆，所以 a!=c，并且我们已经确定它不是一个点，因为 J=ac-b^2!=0）。在这种情况下，椭圆的中心 (x_0,y_0) 由下式给出

p=(b^2)/(sqrt(a^2-b^2))
(27)
=(a^2-c^2)/c
(28)
=(a(1-e^2))/e,
(29)

x_0=(2CD-BE)/(B^2-4AC)

Ellipse4Points

y_0=(2AE-BD)/(B^2-4AC)

|x^2 y^2 x y 1; x_1^2 y_1^2 x_1 y_1 1; x_2^2 y_2^2 x_2 y_2 1; x_3^2 y_3^2 x_3 y_3 1; x_4^2 y_4^2 x_4 y_4 1|=0.
(30)

半轴长度为

s_1s_2s_3+s_1s_2s_4+s_1s_3s_4+s_2s_3s_4-(s_1+s_2+s_3+s_4)=0,
(31)

a^2=(2Delta)/(J(sqrt((A-C)^2+B^2)-(A+C)))

(s_1^4+s_2^4+s_3^4+s_4^4)+(4s_2^2s_3^2s_1^2+s_2^2s_4^2s_1^2+s_3^2s_4^2s_1^2+s_2^2s_3^2s_4^2)-4(s_2s_3s_4s_1^3+s_2s_3s_4^3s_1+s_2s_3^3s_4s_1+s_2^3s_3s_4s_1)-2(s_2^2s_1^2+s_3^2s_1^2+s_4^2s_1^2+s_2^2s_3^2+s_2^2s_4^2-2s_3^2s_4^2)+8s_2s_3s_4s_1. =0
(32)

b^2=(2Delta)/(J(-sqrt((A-C)^2+B^2)-(A+C)))

从 x 轴到椭圆长轴的逆时针旋转角为

e=sqrt(1-(b^2)/(a^2)),
(33)

theta={1/2}cot^(-1)((A-C)/B)

b=asqrt(1-e^2)
(34)
=sqrt(a^2-c^2)
(35)
c=sqrt(a^2-b^2)
(36)
=ae
(37)
e=sqrt(1-(b^2)/(a^2))
(38)
=c/a.
(39)

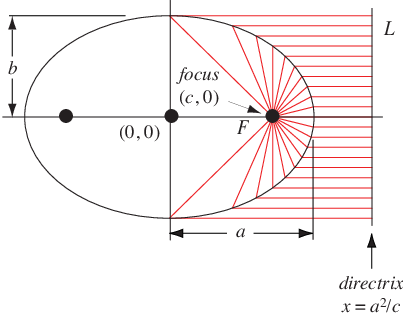
椭圆也可以定义为点的轨迹，这些点到焦点的距离与到称为圆锥曲线准线的垂直线的水平距离成比例，其中比率为 <1。令 r 为比率，d 为准线与中心的距离，那么为了使此成立，它必须在长轴和短轴的极值处成立，因此

EllipseFocus

a=rd

x=c+rcostheta
(40)
y=rsintheta,
(41)

sqrt(a^2-b^2)=r(d-b^2/a)

((c+rcostheta)^2)/(a^2)+(r^2sin^2theta)/(b^2)=1.
(42)

求解得到

b^2(c^2+2crcostheta+r^2cos^2theta)+a^2r^2sin^2theta=a^2b^2.
(43)

r=sqrt(1-b^2/a^2)

b^2c^2+2rcb^2costheta+b^2r^2cos^2theta+a^2r^2-a^2r^2cos^2theta=a^2b^2.
(44)

d=a

a^2(1-e^2)a^2e^2+2aea^2(1-e^2)rcostheta+a^2(1-e^2)r^2cos^2theta +a^2r^2-a^2r^2cos^2theta=a^2[a^2(1-e^2)].
(45)

椭圆的焦参数是

-r^2+[ercostheta-a(1-e^2)]^2=0,
(46)

p=b^2/a

r=+/-[ercostheta-a(1-e^2)].
(47)

其中 e 是椭圆的一个特征，称为离心率，稍后将定义。

r=a(1-e^2)-ercostheta
(48)
r(1+ecostheta)=a(1-e^2)
(49)
r=(a(1-e^2))/(1+ecostheta).
(50)
Ellipsex

轴线平行于坐标轴的椭圆由其上的任意四个非共圆点唯一确定，并且通过四个点 (x_1,y_1), (x_2,y_2), (x_3,y_3), 和 (x_4,y_4) 的椭圆的方程为

costheta=(x-c)/r.
(51)

|x^2,y^2,x,y,1,(x_1^2,y_1^2,x_1,y_1,1),(x_2^2,y_2^2,x_2,y_2,1),(x_3^2,y_3^2,x_3,y_3,1),(x_4^2,y_4^2,x_4,y_4,1)|=0

r+e(x-c)=a(1-e^2)
(52)
r=a(1-e^2)-e(x-c).
(53)

令轴线平行于坐标轴的椭圆上的四个点的角坐标为 t_i，其中 i=1, 2, 3 和 4。当

(b^2)/(p^2)=(2a)/r-1.
(54)

(s_1-s_3)(s_2-s_4)=(s_1-s_4)(s_2-s_3)

s(t)=aE(t,e)
(55)
=aE(t,sqrt(1-(b^2)/(a^2)))
(56)
=bE(t,sqrt(1-(a^2)/(b^2))),
(57)

当中间变量 s_i=tan(t_i/2) 已被定义时，这些点是共圆的（Berger et al. 1984; Trott 2006, pp. 39-40）。相当令人惊讶的是，在简化上述公式后，得到相同的关系，其中 s_i 现在被解释为 s_i=sin(t_i)。一个等效但更复杂的条件由下式给出

sin(t_1+t_3)sint_2sint_4=sin(t_2+t_4)sint_1sint_3

theta=tan^(-1)(y/x)=tan^(-1)(b/atant).
(58)
EllipseFunction

与双曲线一样，非圆椭圆有两个不同的焦点和两个相关的准线，每个圆锥曲线准线都垂直于连接两个焦点的直线（Eves 1965, p. 275）。

kappa(t)=(ab)/((b^2cos^2t+a^2sin^2t)^(3/2))
(59)
phi(t)=tan^(-1)(a/btant).
(60)

定义一个新常数 0<=e<1，称为离心率（其中 e=0 是圆的情况）以替换 b

p=aE(2pi,e)
(61)
=4aE(1/2pi,e)
(62)
=4aE(e),
(63)

e=sqrt(1-b^2/a^2)

p=pi(a+b)sum_(n=0)^(infty)(1/2; n)^2h^(2n)
(64)
=pi(a+b)(1+1/4h^2+1/(64)h^4+1/(256)h^6+...)
(65)

由此得出

h=(a-b)/(a+b).
(66)

b^2=a^2(1-e^2)

p=pi(a+b)_2F_1(-1/2,-1/2;1;h^2)
(67)
=2(a+b)[2E(h)+2(h^2-1)K(h)],
(68)

c=ae

EllipsePerimeter

p=a(1-e^2)

p approx pisqrt(2(a^2+b^2))
(69)
approx pi[3(a+b)-sqrt((a+3b)(3a+b))]
(70)
approx pi(a+b)(1+(3h)/(10+sqrt(4-3h))),
(71)

d=a/e

r=1-e

r_+=r_(apoapsis)=a(1+e)
(72)
r_-=r_(periapsis)=a(1-e).
(73)

r=1+e

A=int_(-a)^aint_(-bsqrt(a^2-x^2)/a)^(bsqrt(a^2-x^2)/a)dydx
(74)
=int_(-a)^a(2b)/asqrt(a^2-x^2)dx
(75)
=(2b)/a{1/2[xsqrt(a^2-x^2)+a^2sin^(-1)(x/(|a|))]}_(x=-a)^a
(76)
=ab[sin^(-1)1-sin^(-1)(-1)]
(77)
=ab[pi/2-(-pi/2)]
(78)
=piab.
(79)

e=c/a

1/(a^2)(a/bx^')^2+(y^('2))/(b^2)=1,
(80)

离心率因此可以解释为焦点的位置，表示为半长轴的一部分。

(partialx)/(partialx^')=((partialx^')/(partialx))^(-1)=(b/a)^(-1)=a/b,
(81)

如果从焦点 F 而不是从中心 C 测量 r 和 theta （在轨道力学中通常是这样），则椭圆方程为

|(partial(x,y))/(partial(x^',y^'))|=|(partialx)/(partialx^') (partialy)/(partialx^'); (partialx)/(partialy^') (partialy)/(partialy^')|
(82)
=|a/b 0; 0 1|=a/b.
(83)

x=r(theta)costheta+ae

intint_(R)dxdy=intint_(R^')|(partial(x,y))/(partial(x^',y^'))|dx^'dy^'
(84)
=a/bintint_(R^')dx^'dy^'
(85)
=a/b(pib^2)
(86)
=piab,
(87)

y=r(theta)sintheta

ax^2+bxy+cy^2=1
(88)

并且 (◇) 变为

A=(2pi)/(sqrt(4ac-b^2)).
(89)

(r(theta)costheta+ae)^2/a^2+(r(theta)sintheta)^2/b^2=1

A=1/2pi(a^2+b^2+|OP|^2).
(90)
EllipseNormalTangent

清除分母得到

x_T(t)=-(asint)/(sqrt(b^2cos^2t+a^2sin^2t))
(91)
y_T(t)=(bcost)/(sqrt(b^2cos^2t+a^2sin^2t)).
(92)

b^2(r(theta)costheta+ae)^2+a^2(r(theta)sintheta)^2=a^2b^2

代入 sin^2theta=1-cos^2theta 得到

b^2(rcostheta+ae)^2+a^2r^2(1-cos^2theta)=a^2b^2

代入以用 a 和 e 重新表达 b 和 c,

a^2(1-e^2)(rcostheta+ae)^2+a^2r^2(1-cos^2theta)=a^4(1-e^2)

r=(a(1-e^2))/(1+ecostheta)

符号可以通过要求 r 必须为正来确定。当 e=0 时，(47) 变为 r=+/-(-a)，但由于 a 始终为正，我们必须取负号，因此 (47) 变为

引用为

Weisstein, Eric W. "Ellipse." 来自 MathWorld--Wolfram Web 资源。 https://mathworld.net.cn/Ellipse.html

主题分类