主题
Search

调和数

DOWNLOAD Mathematica Notebook下载 Wolfram 笔记本
HarmonicNumber

调和数是 以下形式的数

H_n=sum_(k=1)^n1/k
(1)

由截断调和级数产生。调和数可以用解析形式表示为

H_n=gamma+psi_0(n+1),
(2)

其中 gamma 是欧拉-马歇罗尼常数，Psi(x)=psi_0(x) 是双伽玛函数。

前几个调和数 H_n 是 1, 3/2, 11/6, 25/12, 137/60, ... (OEIS A001008 和 A002805)。H_(10^n) 的分子位数，对于 n=0, 1, ... 分别是 1, 4, 41, 434, 4346, 43451, 434111, 4342303, 43428680, ... (OEIS A114467)，相应的分母位数由 1, 4, 40, 433, 4345, 43450, 434110, 4342302, 43428678, ... (OEIS A114468) 给出。这些数字收敛到看起来是 log_(10)e=0.43429448... 的十进制数字 (OEIS A002285)。

HarmonicNumberPrimes

使得 H_n 的分子为素数的前几个索引 n 由 2, 3, 5, 8, 9, 21, 26, 41, 56, 62, 69, ... (OEIS A056903) 给出。对素数分子的搜索已完成至 81780，由 E. W. Weisstein (2009 年 5 月 13 日) 完成，下表总结了已知的最大值。

n十进制位数发现者
6394227795E. W. Weisstein (2007 年 2 月 14 日)
6929430067E. W. Weisstein (2008 年 2 月 1 日)
6992730301E. W. Weisstein (2008 年 3 月 11 日)
7744933616E. W. Weisstein (2009 年 4 月 4 日)
7812833928E. W. Weisstein (2009 年 4 月 9 日)
7899334296E. W. Weisstein (2009 年 4 月 17 日)
8165835479E. W. Weisstein (2009 年 5 月 12 日)

H_n 的分母似乎永远不是素数，除了 H_2=3/2 的情况。此外，分母永远不是素数幂（除了这种情况），因为分母总是可以被小于或等于 n 的最大 2 的幂整除，并且也可以被任何素数 p 整除，其中 n/2<p<=n。

调和数实现为HarmonicNumber[n]。

使得 H_n 等于或超过 1, 2, 3, ... 的 n 值由 1, 4, 11, 31, 83, 227, 616, 1674, ... (OEIS A004080) 给出。另一个有趣的序列是 H_(10^n) 的简单连分数中的项数，对于 n=0, 1, 2, ...，由 1, 8, 68, 834, 8356, 84548, 841817, 8425934, 84277586, ... (OEIS A091590) 给出，据推测它接近 12ln2/pi^2=0.8427659... (OEIS A089729)。

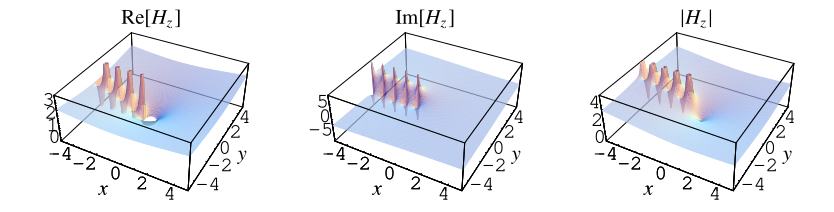
HarmonicNumberReIm
HarmonicNumberContours

调和数的定义也可以扩展到复平面，如上图所示。

根据它们的定义，调和数满足明显的递推方程

H_n=1/n+H_(n-1)
(3)

其中 H_1=1。

在求和中取交替符号形成的数也具有明确的解析形式

H_n^'=sum_(k=1)^(n)((-1)^(k+1))/k
(4)
=ln2+1/2(-1)^n[psi_0(1/2n+1/2)-psi_0(1/2n+1)]
(5)
=ln2+1/2(-1)^n[H_((n-1)/2)-H_(n/2)].
(6)

H_(2n)^' 具有特别优美的形式

H_(2n)^'=sum_(k=1)^(2n)((-1)^(k+1))/k
(7)
=sum_(k=1,3,...)^(2n)((-1)^(k+1))/k+sum_(k=2,4,...)^(2n)((-1)^(k+1))/k
(8)
=sum_(k=1,3,...)^(2n)1/k-sum_(k=2,4,...)^(2n)1/k
(9)
=(sum_(k=1,3,...)^(2n)1/k+sum_(k=2,4,...)^(2n)1/k)-2sum_(k=2,4,...)^(2n)1/k
(10)
=sum_(k=1)^(2n)1/k-sum_(k=1)^(n)1/k
(11)
=H_(2n)-H_n.
(12)

调和数 H_n 永远不是整数，除了 H_1，这可以通过使用强三角不等式来证明，对于 n>1，H_n 的 2-adic 值大于 1。这个结果在 1915 年由 Taeisinger 证明，更一般的结论是，任何数量的连续项（不一定从 1 开始）的和永远不是整数，这在 1918 年由 Kürschák 证明 (Hoffman 1998, p. 157)。

调和数具有奇数分子和偶数分母。n 阶调和数渐近地由下式给出

H_n∼lnn+gamma+1/(2n)-1/(12)n^(-2)+1/(120)n^(-4)-1/(252)n^(-6)+...,
(13)

其中 gamma 是欧拉-马歇罗尼常数 (Conway and Guy 1996; Havil 2003, pp. 79 和 89)，其中一般 (2n) 项是 zeta(1-2n)，给出 -12, 120, -252, 240, ... 对于 n=1, 2, ... (OEIS A006953)。这个公式是 欧拉-麦克劳林积分公式的一个特例 (Havil 2003, p. 79)。

HarmonicNumberInequalities

限制 H_n 的不等式包括

1/(2(n+1))<H_n-lnn-gamma<1/(2n)
(14)

(Young 1991; Havil 2003, pp. 73-75) 和

1/(24(n+1)^2)<H_n-ln(n+1/2)-gamma<1/(24n^2)
(15)

(DeTemple 1991; Havil 2003, pp. 76-78)。

一个有趣的解析和由下式给出

sum_(n=1)^infty(H_n)/(n·2^n)=1/(12)pi^2.
(16)

(Coffman 1987)。Borwein 和 Borwein (1995) 表明

sum_(n=1)^(infty)(H_n^2)/((n+1)^2)=(11)/4zeta(4)=(11)/(360)pi^4
(17)
sum_(n=1)^(infty)(H_n^2)/(n^2)=(17)/4zeta(4)=(17)/(360)pi^4
(18)
sum_(n=1)^(infty)(H_n)/(n^3)=5/4zeta(4)=1/(72)pi^4
(19)
sum_(n=1)^(infty)(H_n)/(n^4)=3zeta(5)-1/6pi^2zeta(3)
(20)
sum_(n=1)^(infty)(H_n)/(n^5)=1/(540)pi^6-1/2[zeta(3)]^2,
(21)

其中 zeta(z) 是黎曼zeta函数。第一个由 de Doelder (1991) 先前推导出来，第三个由 Goldbach 在 1742 年给 Euler 的信中推导出来 (Borwein and Bailey 2003, pp. 99-100; Bailey et al. 2007, p. 256)。这些恒等式是恒等式

1/piint_0^pix^2{ln[2cos(1/2x)]}^2dx=(11)/2zeta(4)=(11)/(180)pi^4
(22)

(Borwein and Borwein 1995) 的推论。Euler 的其他恒等式是

sum_(n=1)^(infty)(H_n)/(n^2)=2zeta(3)
(23)
2sum_(n=1)^(infty)(H_n)/(n^m)=(m+2)zeta(m+1)-sum_(n=1)^(m-2)zeta(m-n)zeta(n+1)
(24)

对于 m=2, 3, ... (Borwein and Borwein 1995)，其中 zeta(3) 是阿佩里常数。这些和与所谓的欧拉和有关。

B. Cloitre (私人通信，2006 年 1 月 7 日) 给出的一个通用恒等式是

sum_(k=1)^infty(H_k)/((k+1)_m)=1/((m-1)!(m-1)^2),
(25)

其中 (x)_n 是波赫哈默尔符号。

Gosper 给出了有趣的恒等式

sum_(i=0)^(infty)(z^iH_i)/(i!)=-e^zsum_(k=1)^(infty)((-z)^k)/(kk!)
(26)
=e^z[lnz+Gamma(0,z)+gamma],
(27)

其中 Gamma(0,z) 是不完全伽玛函数，gamma 是欧拉-马歇罗尼常数。

G. Huvent (2002) 发现了优美的公式

zeta(5)=-(16)/(11)sum_(n=1)^infty([2(-1)^n+1]h_n)/(n^4).
(28)

一个优美的二重级数由下式给出

sum_(k=1)^inftysum_(j=1)^infty(H_j(H_(k+1)-1))/(kj(k+1)(j+k)) =-4zeta(2)-2zeta(3)+4zeta(2)zeta(3)+2zeta(5)
(29)

(Bailey et al. 2007, pp. 273-274)。另一个二重和是

sum_(i=0)^(k-1)sum_(j=k)^n((-1)^(i+j-1))/(j-i)(n; i)(n; j)=sum_(i=1)^(k-1)(n; i)^2(H_(n-i)-H_i)
(30)

对于 1<=k<=n (Sondow 2003, 2005)。

调和数与黎曼猜想之间存在意想不到的联系。

幂 r 中的广义调和数可以通过关系式定义

H_(n,r)=sum_(k=1)^n1/(k^r),
(31)

其中

H_(n,1)=H_n.
(32)

这些数实现为HarmonicNumber[n, r]。

特殊情况 H_(n,2) 的分子被称为沃尔斯滕霍尔姆数。B. Cloitre (私人通信，) 给出了令人惊讶的恒等式

H_(n,2)=1/2sum_(i=1)^nsum_(j=1)^n((i-1)!(j-1)!)/((i+j)!)+3/2sum_(k=1)^n1/(k^2(2k; k))
(33)

它将 H_(n,2) 与 zeta(2) 的著名级数的不定版本联系起来。H_(n,2) 也满足

lim_(n->infty)H_(n,2)=zeta(2)=(pi^2)/6,
(34)

其中 zeta(2) 是黎曼zeta函数。这来自恒等式

H_(n,2)=zeta(2)-gamma_1(n+1),
(35)

其中 gamma_1(z) 是三伽玛函数，因为

lim_(n->infty)gamma_1(n+1)=0.
(36)

对于奇数 r>=3，广义调和数具有显式形式

H_(n,r)=n^(-r)+(psi_(r-1)(n))/(Gamma(r))+zeta(r),
(37)

其中 psi_r(n) 是多伽玛函数，Gamma(r) 是伽玛函数，zeta(r) 是黎曼zeta函数。

2 索引调和数满足恒等式

H_(n,r)=2^(r-1)(H_(2n,r)-H_(2n,r)^')
(38)

(P. Simon，私人通信，2004 年 8 月 30 日)。

广义调和数 H_(n,r) 的和包括

sum_(n=1)^inftyH_(n,r)z^n=(Li_r(z))/(1-z)
(39)

对于 |z|<1，其中 Li_r(z) 是多重对数函数，

sum_(k=1)^(infty)(H_(k,1))/(k(z+1)^k)=-Li_2(-1/z)
(40)
sum_(k=1)^(infty)(H_(k,1))/(kphi^(2k))=1/(15)pi^2-1/2[csch^(-1)2]^2
(41)
sum_(k=1)^(infty)(H_(k,1))/(k^22^k)=zeta(3)-1/(12)pi^2ln2
(42)
sum_(k=1)^(infty)(H_(k,2))/(k^4)=[zeta(3)]^2-(pi^6)/(2835)
(43)
sum_(k=1)^(infty)(H_(k,2))/(k2^k)=5/8zeta(3)
(44)
sum_(k=1)^(infty)(H_(k,4))/(k^2)=(37pi^6)/(11340)-[zeta(3)]^2,
(45)

其中方程 (40), (41), (42), 和 (44) 归功于 B. Cloitre (私人通信，2004 年 10 月 4 日) 和 Li_2(z) 是双对数函数。一般而言，

sum_(k=1)^infty(H_(k,r))/(k^r)=1/2{[zeta(r)]^2+zeta(2r)}
(46)

(P. Simone，私人通信，2003 年 6 月 2 日)。幂调和数也遵循意想不到的恒等式

9H_(8,n)-19H_(9,n)+10H_(10,n)+sum_(k=1)^(n-1)[H_(8,n-k)H_(9,k)-H_(9,n-k)H_(9,k) -H_(8,n-k)H_(10,k)+H_(9,n-k)H_(10,k)]=0
(47)

(M. Trott，私人通信)。

P. Simone (私人通信，2004 年 8 月 30 日) 表明

[C(t)]^2+[S(t)]^2=1/(90)pi^4+2/3pi^2C(t) -2sum_(m=1)^infty((H_(m,2))/(m^2)+(2H_m)/(m^3))cos(mt),
(48)

其中

C(t)=sum_(n=1)^(infty)(cos(nt))/(n^2)
(49)
=1/2[Li_2(e^(-it))+Li_2(e^(it))]
(50)
S(t)=sum_(n=1)^(infty)(sin(nt))/(n^2)
(51)
=1/2i[Li_2(e^(-it))-Li_2(e^(it))].
(52)

这给出了特殊结果

sum_(n=1)^infty(H_n)/(n^3)=1/(72)pi^4 1/8sum_(n=1)^infty((2H_(4k,2))/(k^2)+(H_(2k))/(k^3))=(211pi^4)/(11520)-K^2 2sum_(k=1)^infty[((-1)^(k+1)H_(k,2))/(k^2)+(2(-1)^(k+1)H_k)/(k^3)]=(37pi^4)/(720)
(53)

对于 t=0,pi/2,pi，分别。

Conway 和 Guy (1996) 将二阶调和数定义为

H_n^((2))=sum_(i=1)^(n)H_i
(54)
=(n+1)(H_(n+1)-1)
(55)
=(n+1)(H_(n+1)-H_1),
(56)

三阶调和数定义为

H_n^((3))=sum_(i=1)^nH_i^((2))=(n+2; 2)(H_(n+2)-H_2),
(57)

并且 k 阶调和数定义为

H_n^((k))=(n+k-1; k-1)(H_(n+k-1)-H_(k-1)).
(58)

Roman (1992) 在与调和对数的联系中给出了一个稍微不同的双索引调和数 c_n^((j)) 的定义。Roman (1992) 将其定义为

c_n^((0))={1 for n>=0; 0 for n<0
(59)
c_0^((j))={1 for j=0; 0 for j!=0
(60)

加上递推关系

c_n^((j))=c_n^((j-1))+nc_(n-1)^((j)).
(61)

对于一般 n>0 和 j>0，这等价于

c_n^((j))=sum_(i=1)^n1/ic_i^((j-1)),
(62)

对于 n>0，它简化为

c_n^((j))=sum_(i=1)^n(n; i)(-1)^(i-1)i^(-j).
(63)

对于 n<0，调和数可以写成

c_n^((j))=(-1)^j|_n]!s(-n,j),
(64)

其中 |_n]! 是罗马阶乘，s 是第一类斯特林数。

另一种有时也称为“调和数”的数是调和除数（或 Ore 数）。

参见

阿佩里常数, 叠书问题, 埃及分数, 欧拉和, 法ulhaber公式, 调和除数, 调和对数, 调和级数, 单位分数, 沃尔斯滕霍尔姆数

相关 Wolfram 网站

http://functions.wolfram.com/GammaBetaErf/HarmonicNumber/, http://functions.wolfram.com/GammaBetaErf/HarmonicNumber2/

此条目的部分内容由 Jonathan Sondow (作者链接) 贡献

使用 Wolfram|Alpha 探索

参考文献

Bailey, D. H.; Borwein, J. M.; Calkin, N. J.; Girgensohn, R.; Luke, D. R.; and Moll, V. H. Experimental Mathematics in Action. Wellesley, MA: A K Peters, 2007.Borwein, J. and Bailey, D. Mathematics by Experiment: Plausible Reasoning in the 21st Century. Wellesley, MA: A K Peters, 2003.Borwein, D. and Borwein, J. M. "On an Intriguing Integral and Some Series Related to zeta(4)." Proc. Amer. Math. Soc. 123, 1191-1198, 1995.Coffman, S. W. "Problem 1240 and Solution: An Infinite Series with Harmonic Numbers." Math. Mag. 60, pp. 118-119, 1987.Conway, J. H. and Guy, R. K. The Book of Numbers. New York: Springer-Verlag, pp. 143 和 258-259, 1996.de Doelder, P. J. "On Some Series Containing Psi(x)-Psi(y) and (Psi(x)-Psi(y))^2 for Certain Values of x and y." J. Comp. Appl. Math. 37, 125-141, 1991.DeTemple, D. W. "The Non-Integer Property of Sums of Reciprocals of Consecutive Integers." Math. Gaz. 75, 193-194, 1991.Flajolet, P. and Salvy, B. "Euler Sums and Contour Integral Representation." Experim. Math. 7, 15-35, 1998.Graham, R. L.; Knuth, D. E.; and Patashnik, O. "Harmonic Numbers" and "Harmonic Summation." §6.3 和 6.4 in Concrete Mathematics: A Foundation for Computer Science, 2nd ed. Reading, MA: Addison-Wesley, pp. 272-282, 1994.Gosper, R. W. "harmonic Summation and exponential gfs." [email protected] posting, Aug. 2, 1996.Havil, J. Gamma: Exploring Euler's Constant. Princeton, NJ: Princeton University Press, 2003.Hoffman, P. The Man Who Loved Only Numbers: The Story of Paul Erdős and the Search for Mathematical Truth. New York: Hyperion, 1998.Huvent, G. "Autour de la primitive de t^pcoth(alphat/2)." Feb. 3, 2002. http://perso.orange.fr/gery.huvent/articlespdf/Autour_primitive.pdf.Roman, S. "The Logarithmic Binomial Formula." Amer. Math. Monthly 99, 641-648, 1992.Roman, S. The Umbral Calculus. New York: Academic Press, p. 99, 1984.Savio, D. Y.; Lamagna, E. A.; and Liu, S.-M. "Summation of Harmonic Numbers." In Computers and Mathematics (Ed. E. Kaltofen and S. M. Watt). New York: Springer-Verlag, pp. 12-20, 1989.Sloane, N. J. A. Sequences A001008/M2885, A002285/M3210, A002805/M1589, A004080, A006953/M2039, A056903, A082912, A089729, A091590, A096618, A114467, and A114468 in "The On-Line Encyclopedia of Integer Sequences."Sondow, J. "Criteria for Irrationality of Euler's Constant." Proc. Amer. Math. Soc. 131, 3335-3344, 2003.Sondow, J. "Problem 11026: An Identity Involving Harmonic Numbers." Amer. Math. Monthly 112, 367-369, 2005.Trott, M. "The Mathematica Guidebooks Additional Material: Harmonic Numbers Inversion." http://www.mathematicaguidebooks.org/additions.shtml#S_3_06.Young, R. M. "Euler's Constant." Math. Gaz. 75, 187-190, 1991.

Wolfram|Alpha 参考

调和数

引用为

Sondow, Jonathan 和 Weisstein, Eric W. "调和数." 来自 MathWorld--Wolfram Web 资源。 https://mathworld.net.cn/HarmonicNumber.html

主题分类