Tanc 函数

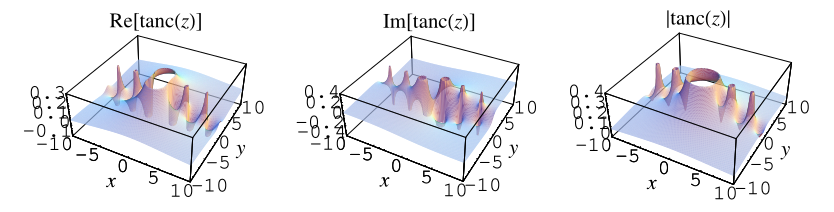
与 sinc 函数 类似，定义 tanc 函数为

(1)

由于 不是一个 基数函数，与 sinc 函数 的“类比”是功能结构上的，而不是数学性质上的。可能存在比此处引入的 更好的术语，尽管似乎以前没有给这个函数分配名称。

导数 由下式给出

(2)

不定积分 显然不能用 闭合形式，以传统定义的函数表示。

此函数常出现在物理学问题中，在这些问题中，需要确定 的值，使得 ，即 。这是一个超越方程，其前几个解在下表中给出，并在上面进行了说明。

	OEIS	根
0		0
1	A115365	4.4934094579090641753...
2		7.7252518369377071642...
3		10.904121659428899827...
4		14.066193912831473480...
5		17.220755271930768739...

这些解的第一个可以用闭合形式给出，如下所示

(3)

其中 是 第一类贝塞尔函数 的第 个正根。

正解可以显式地写成级数形式为

(4)

(OEIS A079330 和 A088989)，其中 中的级数可以通过 级数反演 找到，针对 的级数和

(5)

对于 为 正整数 (D. W. Cantrell, 私人通讯, 1 月 3 日, 2003)。在实践中，级数的前三项通常足以获得近似解。

由于 在 的奇数倍数处的垂直渐近线，这个函数远不如 sinc 函数 表现良好，即使当 时也是如此。上面的图显示了整数 的 。给出 增量最小值的 值是 , 11, 1317811389848379909481978463177998812826691414678853402757616, ...(OEIS A079331), 对应于 , , , , .... 类似地，给出 增量最大值的 值是 , 122925461, 534483448, 3083975227, 214112296674652, ... (OEIS A079332), 对应于 1.55741, 2.65934, 3.58205, 4.3311, 18.0078, 18.0566, 556.306, ... (D. W. Cantrell, 私人通讯, 1 月 3 日, 2002)。下表 (P. Carmody, 私人通讯, 11 月 21 日, 2003) 将这些结果扩展到连分数的第 194,000 项。所有这些极值都对应于 的连分数展开式的分子。此外，由于它们必须接近 的奇数倍数，以便 很大，因此相应的分母必须是奇数。 的值与连分数展开式中后续项的值之间也存在非常强的相关性 (即，那里的高值意味着先前的收敛值是对 的良好近似)。

最小值	收敛值	最大值
	1	1.55741
	2
	4
	15	2.659341
	17	3.582052
	19	4.331096
	29	18.007800
	118
	136
	233	18.056613
	315	556.306227
	1134
	1568
	1718
	2154
	2468
	3230
	3727	2750.202396
	3763	10539.847388
	5187
	8872
	9768
	11282
	12284
	15503	24263.751532
	24604
	153396
	156559	228085.415076

最大值和最小值的序列几乎可以肯定地是无界的，但尚不知道如何证明这一事实。