增广是截断的对偶操作,它用高度为 (其中
可以是正数、零或负数)的棱锥替换多面体的面(Cromwell 1997,第 124 页和 195-197 页)。该操作有时也称为堆积、akisation(因为它将正多边形转换为
-akis 多面体,即,面数变为四倍)、加帽或累积。
B. Grünbaum 使用术语 elevatum 和 invaginatum 分别表示增广中使用的正高度(向外指向)和负高度(向内指向)棱锥。
术语“增广”有时也用于更广泛的上下文中,指在一个基本立体的面上附加一个多面体帽。一个例子是称为增广截角立方体的约翰逊多面体,其中附加的形状是正方形圆顶——而不是棱锥。
增广在错误的名称下实现Stellate[poly, ratio] 在 Wolfram 语言 包中PolyhedronOperations`并在 Wolfram 语言 中实现为AugmentedPolyhedron[poly]。
矿物学家给出了规则立体的增广形式的以下特殊名称(Berry 和 Mason 1959,第 124 页和 127 页)。
使用 进行增广给出了原始立体的三角剖分版本。下图说明了从负到正增广高度的 柏拉图立体 的增广系列。
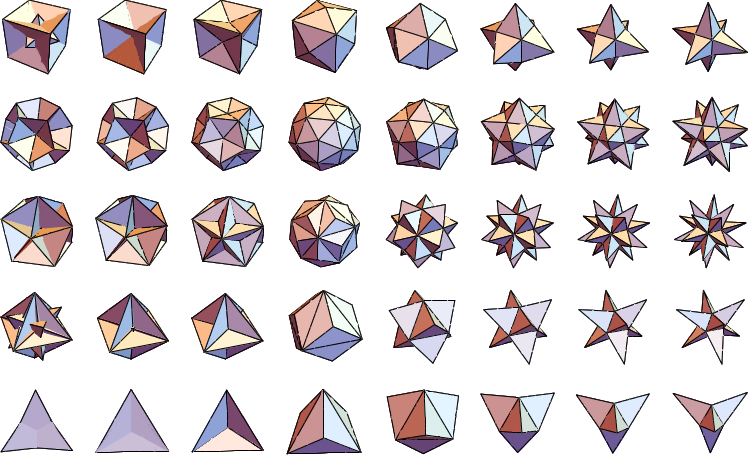
下图和表格给出了在边长为单位的 柏拉图立体 上通过给定高度的增广形成的特殊立体。
| 原始 | 增广 | |
| 立方体 | 四角六面体 | |
| 立方体 | 菱形十二面体 | |
| 立方体 | 星形 等边 24-三角面体 | |
| 正十二面体 | 五角十二面体 | |
| 正十二面体 | 星形 等边 60-三角面体 | |
| 正十二面体 | 小星形十二面体 | |
| 正二十面体 | 大十二面体 | |
| 正二十面体 | 小三方二十面体 | |
| 正二十面体 | 星形 等边 60-三角面体 | |
| 正二十面体 | 大星形十二面体 | |
| 正八面体 | 小三方八面体 | |
| 正八面体 | 星状八面体 | |
| 正四面体 | 三方四面体 | |
| 正四面体 | 立方体 | |
| 正四面体 | 星形 等边 12-三角面体 |

|

|

|

|
上面的顶部图像显示了一个折纸增广四面体和增广十二面体。 它们使用三角形边缘模块构建,并以类似于 Gurkewitz 和 Arnstein (1995, p. 53) 描述的其他实体的方式构建。 左下方的图显示了一个向内增广的十二面体(Fusè 1990,pp. 126-129),对应于 二十面体星状体 (number 26) in Coxeter et al. (1999, pp. 43 and 64),而右图显示了 E. W. Weisstein 构建的增广二十面体(Kasahara 和 Takahama 1987,p. 45)。