（第一）菱形十二面体是 立方八面体 的 对偶多面体 (Holden 1971, p. 55)。它有时也被称为菱面体十二面体 (Cotton 1990)，并且在需要将其与 Bilinski 十二面体 (Bilinski 1960, Chilton and Coxeter 1963) 区分开来时，可能会包含“第一”。上面展示了它的图形，以及线框版本和一个可用于其构建的 网格。
它是 Wenninger 对偶 
。
菱形十二面体在 Wolfram 语言 中实现为PolyhedronData["RhombicDodecahedron"].
菱形十二面体出现在右上角，作为 M. C. Escher 1948 年木刻版画“星星” (Forty 2003, Plate 43) 中的多面体“星星”之一。
菱形十二面体的 14 个顶点由 12 个 菱形 连接而成，尺寸如下图所示，其中
 |  |  |
(1)
|
 |  |  |
(2)
|
 |  |  |
(3)
|
 |  |  |
(4)
|
 |  |  |
(5)
|
|
|
|
菱形十二面体可以通过在一个中心立方体的面上放置六个立方体，以金属“杰克”的配置（左图）构建而成。然后，将外部立方体的中心与中心立方体的顶点连接起来，即可得到菱形十二面体（中图）。在边长为单位长度的 立方体 的每个面上贴上高度为 1/2 的 正方锥体，即可得到菱形十二面体（右图；Brückner 1900, p. 130；Steinhaus 1999, p. 185）。
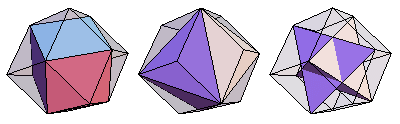
连接菱形十二面体的长对角线（上图中蓝色所示）会得到 八面体 的边，而短对角线则会得到 立方体 的边（红色）。
更具体地说，立方体、八面体 和 星形八面体 可以内接于菱形十二面体的顶点 (E. Weisstein, Dec. 25, 2009)。
菱形十二面体是 立方体-八面体复合体 和第一个 立方八面体星状体 的 凸包。
如果菱形十二面体沿着三个连续的面对角线铰接成六个正方锥体，则所得模型可以折叠成一个立方体 (Wells 1991)。菱形十二面体的一种可能的构造称为 Bauspiel。它也可以通过将单位边长的 立方体 增广 一个高度为 1/2 的锥体来构造。
菱形十二面体是 带状多面体 和 空间填充多面体 (Steinhaus 1999, p. 185)。顶点由 (
, 
, 
), (
, 0, 0), (0, 
, 0), (0, 0, 
) 给出。
|
|
在上面绘制的点中 相交 的 立方体-八面体复合体 的边是 菱形 的对角线（左图），而 12 个 菱形 形成菱形十二面体（中心图；Ball 和 Coxeter 1987）。立方八面体 可以内接于菱形十二面体（右图；Steinhaus 1999, p. 206）。
菱形十二面体有三种星状体。
菱形十二面体可以使用 Haűy 构造 构建。Haűy 菱形十二面体数
 |
(6)
|
给出了一种计算菱形十二面体 体积 的方法，
 |  |  |
(7)
|
 |  |  |
(8)
|
（Steinhaus 1999）。单位边长的菱形十二面体的 表面积 为
 |
(9)
|
其惯性张量为
![I=[1/3Ma^2 0 0; 0 1/3Ma^2 0; 0 0 1/3Ma^2].](/images/equations/RhombicDodecahedron/NumberedEquation3.svg) |
(10)
|
." §3.8.1 in 