小三八面体

通常，三八面体是非正规的二十四面体，可以构造为正八面体的正增广。这种立体也称为三方八面体，尤其是在矿物学家中（Correns 1949，第41页；Berry and Mason 1959，第127页）。虽然由此产生的二十四面体不是正规的，但其面都是相同的。

制作您自己的小三八面体

打印并折叠

3D 打印

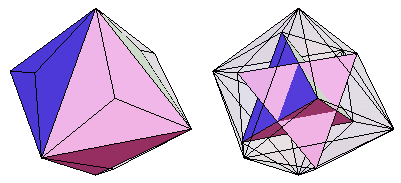
小三八面体，被 Holden (1971, p. 55) 简称为三八面体，是截角立方体的24面对偶多面体，也是 Wenninger 对偶 。添加“小”字是为了将其与大三八面体区分开来，后者是星形截角六面体的对偶。上面展示了它，以及线框版本和一个可用于其构造的网格。

小三八面体可以通过单位边长的八面体的增广来构造，增广的棱锥高度为 。

小三八面体出现在 M. C. Escher 1948 年的木刻版画“星星”的中间右侧，作为多面体“星星”之一（Forty 2003，图版 43）。

它在 Wolfram 语言中实现为PolyhedronData["SmallTriakisOctahedron"].

小三八面体是等边增广立方体的凸包。

八面体和星形八面体可以内接在小三八面体的顶点上（E. Weisstein，2009 年 12 月 25 日）。

小三八面体的对偶多面体是截角立方体，两者都与它们的公共中球一起在上面展示。对于单位边长的截角立方体，其对偶的边长为

			(1)
			(2)

归一化使得 ，得到的小三八面体的表面积和体积为

			(3)
			(4)