正交群

对于每个维度 ，正交群 是 正交矩阵的群。这些矩阵构成一个群，因为它们在乘法和取逆运算下是封闭的。

将矩阵视为由 坐标函数给出，矩阵集合等同于 。正交矩阵是 个方程的解

(1)

其中 是单位矩阵，这些方程是冗余的。其中只有 个是独立的，剩下 个“自由变量”。实际上，正交群是一个光滑的 维子流形。

由于正交群是群和流形，因此它是李群。 在单位元处有一个子流形切空间，它是反对称矩阵 的李代数。实际上，正交群是一个紧李群。

行列式一个正交矩阵的行列式为 1 或 ，因此正交群有两个连通分支。包含单位元的连通分支是特殊正交群 。例如，群 在平面上的群作用是旋转

(2)

其中 是 中的任意实数。这些矩阵保持二次形式 不变，因此它们也保持圆 不变，这些圆是群轨道。

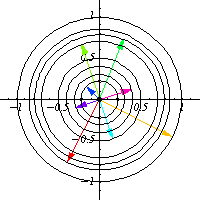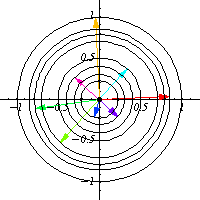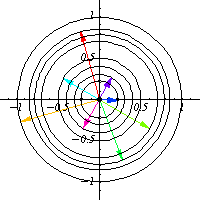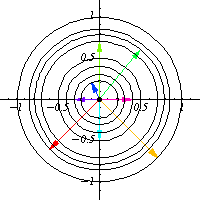
作为流形， 由圆的两个不相交的副本组成。

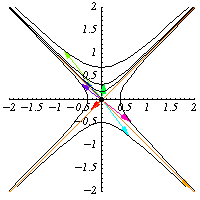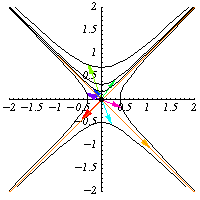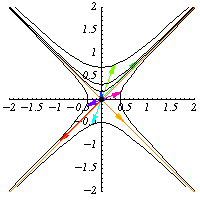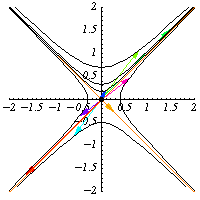
正交群有几种推广。首先，可以为任何具有矩阵签名 的对称二次型 定义正交群。保持 不变的矩阵 的群，即，

(3)

被记为 。洛伦兹群是 。例如，矩阵

(4)

是 的元素。它们保持二次形式 不变，因此它们保持双曲线 不变。

除了使用实数作为系数，还可以使用来自任何域 的系数，在这种情况下，它被记为 。正交矩阵仍然满足 。例如， 包含

(5)

并且总共有 48 个元素。

当然， 表示保持具有矩阵签名 的对称二次型的矩阵群，其系数在域 中。当 不是 或 时，这些群被称为李型群。

当系数是复数时，它被称为复正交群，它与酉群非常不同。例如，形式为

(6)

的矩阵在 中。特别地， 不是紧李群。在仿射空间中定义 的方程是二次多项式。因此， 是线性代数群。

正交群 中阶数为 , 2, 3, ... 的子群数量 是 1, 3, 1, 5, 1, 5, 1, 7, 1, 5, 1, 8, ... (OEIS A001051)，即 {1,5,1,7} 的重复序列，例外情况为 , , , , 以及 。