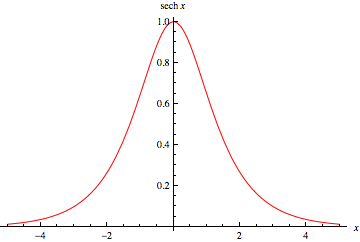
双曲正割定义为
其中  是双曲余弦。它在 Wolfram 语言 中被实现为Sech[z]。
是双曲余弦。它在 Wolfram 语言 中被实现为Sech[z]。
在实数线上,它在  处有最大值,拐点在
处有最大值,拐点在  (OEIS A091648)。它在
(OEIS A091648)。它在  处有一个不动点 (OEIS A069814)。
处有一个不动点 (OEIS A069814)。
导数由下式给出
 |
(3)
|
其中  是双曲正切,不定积分由下式给出
是双曲正切,不定积分由下式给出
![intsechzdz=2tan^(-1)[tanh(1/2z)]+C,](/images/equations/HyperbolicSecant/NumberedEquation2.svg) |
(4)
|
其中  是积分常数。
是积分常数。
 具有泰勒级数
具有泰勒级数
(OEIS A046976 和 A046977),其中  是欧拉数,
是欧拉数, 是阶乘。
是阶乘。
在拉马努金 cos/cosh 恒等式中,将  ,
,  , 和
, 和  的系数相等
的系数相等
![[1+2sum_(n=1)^infty(cos(ntheta))/(cosh(npi))]^(-2)+[1+2sum_(n=1)^infty(cosh(ntheta))/(cosh(npi))]^(-2)=(2Gamma^4(3/4))/pi](/images/equations/HyperbolicSecant/NumberedEquation3.svg) |
(7)
|
给出惊人的恒等式
![sum_(n=1)^inftysech(pin)=1/2{(sqrt(pi))/([Gamma(3/4)]^2)-1}
sum_(n=1)^inftyn^4sech(pin)=(18[Gamma(3/4)]^2)/(sqrt(pi))[sum_(n=1)^inftyn^2sech(pin)]^2
sum_(n=1)^inftyn^8sech(pin)=(168[Gamma(3/4)]^2)/(sqrt(pi))[sum_(n=1)^inftyn^2sech(pin)]×sum_(n=1)^inftyn^6sech(pin)-(63000[Gamma(3/4)]^6)/(pi^(3/2))[sum_(n=1)^inftyn^2sech(pin)]^4.](/images/equations/HyperbolicSecant/NumberedEquation4.svg) |
(8)
|
另请参阅
Benson 公式,
悬链线,
悬链面,
欧拉数,
高斯函数,
双曲余弦,
双曲函数,
反双曲正割,
洛伦兹函数,
扁球面坐标,
伪球面,
正割,
旋转曲面,
曳物线,
阿涅西的女巫曲线
使用 探索
参考文献
Abramowitz, M. and Stegun, I. A. (Eds.). "Hyperbolic Functions." §4.5 in Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, 9th printing. New York: Dover, pp. 83-86, 1972.Jeffrey, A. "Hyperbolic Identities." §2.5 in Handbook of Mathematical Formulas and Integrals, 2nd ed. Orlando, FL: Academic Press, pp. 117-122, 2000.Sloane, N. J. A. Sequences A046976, A046977, A069814, and A091648 in "The On-Line Encyclopedia of Integer Sequences."Spanier, J. and Oldham, K. B. "The Hyperbolic Secant  and Cosecant
and Cosecant  Functions." Ch. 29 in An Atlas of Functions. Washington, DC: Hemisphere, pp. 273-278, 1987.Zwillinger, D. (Ed.). "Hyperbolic Functions." §6.7 in CRC Standard Mathematical Tables and Formulae. Boca Raton, FL: CRC Press, pp. 476-481 1995.
Functions." Ch. 29 in An Atlas of Functions. Washington, DC: Hemisphere, pp. 273-278, 1987.Zwillinger, D. (Ed.). "Hyperbolic Functions." §6.7 in CRC Standard Mathematical Tables and Formulae. Boca Raton, FL: CRC Press, pp. 476-481 1995.在 上被引用
双曲正割
请引用为
Weisstein, Eric W. “双曲正割。” 来自 Web 资源。 https://mathworld.net.cn/HyperbolicSecant.html
主题分类
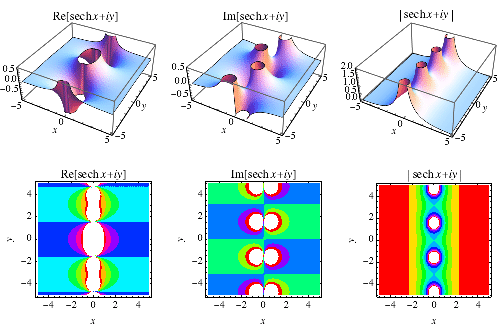
是双曲余弦。它在 Wolfram 语言 中被实现为Sech[z]。
处有最大值,拐点在
(OEIS A091648)。它在
处有一个不动点 (OEIS A069814)。
是积分常数。
具有泰勒级数
是欧拉数,
是阶乘。
,
, 和
的系数相等
![[1+2sum_(n=1)^infty(cos(ntheta))/(cosh(npi))]^(-2)+[1+2sum_(n=1)^infty(cosh(ntheta))/(cosh(npi))]^(-2)=(2Gamma^4(3/4))/pi](/images/equations/HyperbolicSecant/NumberedEquation3.svg)
![sum_(n=1)^inftysech(pin)=1/2{(sqrt(pi))/([Gamma(3/4)]^2)-1}
sum_(n=1)^inftyn^4sech(pin)=(18[Gamma(3/4)]^2)/(sqrt(pi))[sum_(n=1)^inftyn^2sech(pin)]^2
sum_(n=1)^inftyn^8sech(pin)=(168[Gamma(3/4)]^2)/(sqrt(pi))[sum_(n=1)^inftyn^2sech(pin)]×sum_(n=1)^inftyn^6sech(pin)-(63000[Gamma(3/4)]^6)/(pi^(3/2))[sum_(n=1)^inftyn^2sech(pin)]^4.](/images/equations/HyperbolicSecant/NumberedEquation4.svg)