“阿涅西的女巫曲线”是由玛丽亚·阿涅西于 1748 年在她的著作《Instituzioni analitiche ad uso della gioventù italiana 》(第一部由女性撰写的现存数学著作)中研究的曲线。这条曲线也被称为阿涅西三次曲线或阿涅西曲线,并且早先在 1703 年已被费马和圭多·格兰迪研究过。
“女巫”这个名字源于对原始著作中术语 averisera (“正矢曲线”,来自拉丁语 vertere ,“转动”)的误译,在 1801 年剑桥卢卡斯数学教授约翰·科尔森 (Gray) 对该著作的翻译中,被误译为 avversiera (“女巫”或“魔鬼的妻子”)。
该曲线是通过从原点绘制一条线
参数形式为,
对于
对于
笛卡尔方程可以通过在参数方程中消去
(5)
这在函数形式上等价于洛伦兹函数 。
曲线与
(6)
该曲线在 拐点 。直线 渐近线 。
第二种参数化中的曲率 和切线角 由下式给出
另请参阅 高斯函数 ,
双曲正割 ,
拉梅曲线 ,
洛伦兹函数
使用 探索
参考文献 Beyer, W. H. CRC Standard Mathematical Tables, 28th ed. Gray, S. "History of the Name 'Witch.' " http://instructional1.calstatela.edu/sgray/Agnesi/WitchHistory/Historynamewitch.html . Lawrence, J. D. A Catalog of Special Plane Curves. MacTutor History of Mathematics Archive. "Witch of Agnesi." http://www-groups.dcs.st-and.ac.uk/~history/Curves/Witch.html . Smith, D. E. History of Mathematics, Vol. 2: Special Topics of Elementary Mathematics. Yates, R. C. "Witch of Agnesi." A Handbook on Curves and Their Properties.
请引用为
韦斯坦因,埃里克·W. "阿涅西的女巫曲线。" 来自 https://mathworld.net.cn/WitchofAgnesi.html
主题分类
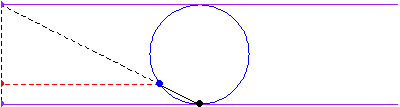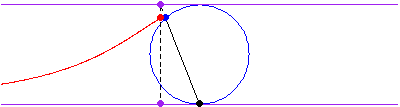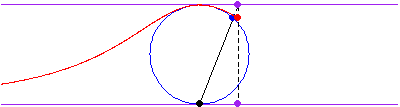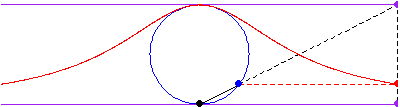
,穿过半径为
,中心为
的圆而获得的,然后选取与圆的交点的
坐标,以及线
的延长线与直线
的交点的
坐标来确定曲线上的点。
, 或
.
得到,为
轴之间的面积为

![-tan^(-1)[(2t)/((1+t^2)^2)].](/images/equations/WitchofAgnesi/Inline31.svg)