主题
Search

高斯函数

DOWNLOAD Mathematica Notebook下载 Wolfram Notebook
GaussianReal
最小值 最大值
Powered by webMathematica
GaussianReImAbs
最小值 最大值
实部
虚部 Powered by webMathematica

在一维中，高斯函数是 概率密度函数 的 正态分布，

f(x)=1/(sigmasqrt(2pi))e^(-(x-mu)^2/(2sigma^2)),
(1)

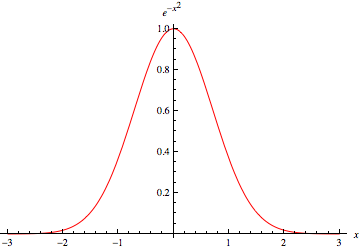
有时也称为 频率曲线。 半峰全宽 (FWHM) 是通过找到半最大值点 x_0 找到的。 常数比例因子可以忽略，所以我们必须求解

e^(-(x_0-mu)^2/(2sigma^2))=1/2f(x_(max))
(2)

但 f(x_(max)) 发生在 x_(max)=mu，所以

e^(-(x_0-mu)^2/(2sigma^2))=1/2f(mu)=1/2.
(3)

求解，

e^(-(x_0-mu)^2/(2sigma^2))=2^(-1)
(4)
-((x_0-mu)^2)/(2sigma^2)=-ln2
(5)
(x_0-mu)^2=2sigma^2ln2
(6)
x_0=+/-sigmasqrt(2ln2)+mu.
(7)

因此，半峰全宽 由下式给出

FWHM=x_+-x_-=2sqrt(2ln2)sigma approx 2.3548sigma.
(8)
GaussianFunction2D

在二维中，圆形高斯函数是不相关变量 X 和 Y 的分布函数，这些变量具有 二元正态分布 和相等的 标准差 sigma=sigma_x=sigma_y，

f(x,y)=1/(2pisigma^2)e^(-[(x-mu_x)^2+(y-mu_y)^2]/(2sigma^2)).
(9)

相应的椭圆高斯函数对应于 sigma_x!=sigma_y，由下式给出

f(x,y)=1/(2pisigma_xsigma_y)e^(-[(x-mu_x)^2/(2sigma_x^2)+(y-mu_y)^2/(2sigma_y^2)]).
(10)
GaussianApodization

高斯函数也可以用作 切趾函数

A(x)=e^(-x^2/(2sigma^2)),
(11)

如上所示，带有相应的 仪器函数。仪器函数是

I(k)=e^(-2pi^2k^2sigma^2)sigmasqrt(pi/2)[erf((a-2piiksigma^2)/(sigmasqrt(2)))+erf((a+2piiksigma^2)/(sigmasqrt(2)))],
(12)

其最大值为

I_(max)=sigmasqrt(2pi)erf(a/(sigmasqrt(2))).
(13)

当 a->infty 时，方程 (12) 简化为

lim_(a->infty)I(k)=sigmasqrt(2pi)e^(-2pi^2k^2sigma^2).
(14)

超几何函数有时也称为高斯函数。

另请参阅

二元正态分布, Erf, Erfc, 傅里叶变换--高斯, 双曲正割, 洛伦兹函数, 正态分布, Owen T 函数, 阿涅西的女巫曲线

使用 Wolfram|Alpha 探索

参考文献

MacTutor History of Mathematics Archive. "频率曲线。" http://www-groups.dcs.st-and.ac.uk/~history/Curves/Frequency.html。

在 Wolfram|Alpha 上被引用

高斯函数

请引用为

Weisstein, Eric W. "高斯函数。" 来自 MathWorld--Wolfram Web 资源。 https://mathworld.net.cn/GaussianFunction.html

主题分类