主题
Search

洛伦兹函数

DOWNLOAD Mathematica Notebook下载 Wolfram Notebook
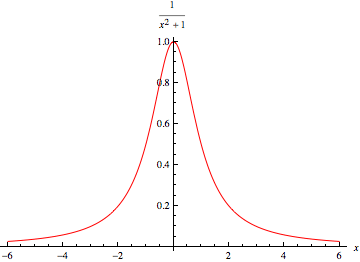
LorentzianReal
最小值 最大值
Powered by webMathematica

洛伦兹函数是由以下单峰函数给出：

L(x)=1/pi(1/2Gamma)/((x-x_0)^2+(1/2Gamma)^2),
(1)

其中 x_0 是中心，Gamma 是指定宽度的参数。 洛伦兹函数被归一化，使得

int_(-infty)^inftyL(x)=1.
(2)

它在 x=x_0 处有最大值，其中

L^'(x)=-(16(x-x_0)Gamma)/(pi[4(x-x_0)^2+Gamma^2]^2)=0.
(3)

它在最大值处的值是

L(x_0)=2/(piGamma).
(4)

它在

x=(x_0+/-1/2Gamma),
(5)

处等于其最大值的一半，因此具有半峰全宽 Gamma。 该函数在

L^('')(x)=16Gamma(12(x-x_0)^2-Gamma^2)/(pi[4(x-x_0)^2+Gamma^2]^3)=0,
(6)

处有拐点，给出

x_1=x_0-1/6sqrt(3)Gamma,
(7)

其中

L(x_1)=3/(2piGamma).
(8)
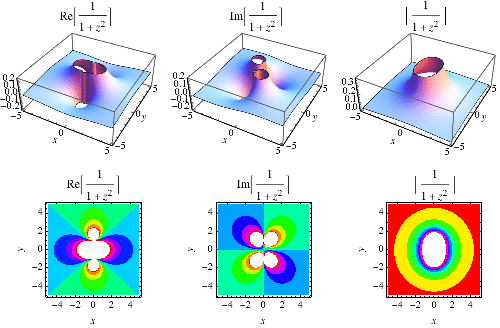LorentzianReImAbs
最小值 最大值
实部
虚部 Powered by webMathematica

扩展到复平面的洛伦兹函数如上图所示。

洛伦兹函数给出了某些类型谱线的形状，并且是柯西分布中的分布函数。 洛伦兹函数具有傅里叶变换

F_x[1/pi(1/2Gamma)/((x-x_0)^2+(1/2Gamma)^2)](k)=e^(-2piikx_0-Gammapi|k|).
(9)
LorentzianApodization

洛伦兹函数也可以用作孔径函数，尽管其仪器函数在解析上难以表达。

另请参阅

柯西分布, 阻尼指数余弦积分, 傅里叶变换--洛伦兹函数, 高斯函数, 双曲正割, 逻辑分布, 阿涅西的女巫线

使用 Wolfram|Alpha 探索

引用为

Weisstein, Eric W. "洛伦兹函数。" 来自 MathWorld--Wolfram Web 资源。 https://mathworld.net.cn/LorentzianFunction.html

主题分类