渐开线

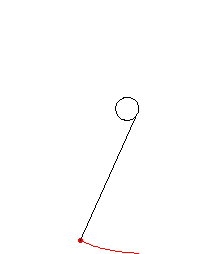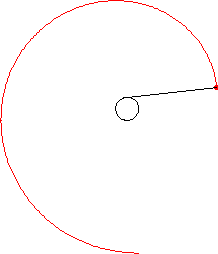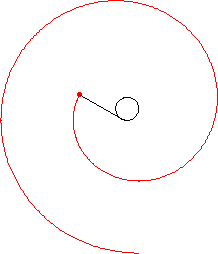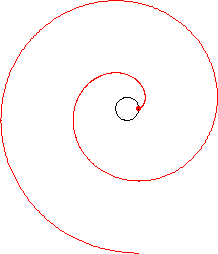
将一根绳子连接到曲线上的一个点。拉伸绳子，使其与曲线在该连接点相切。然后将绳子缠绕起来，始终保持绷紧。绳子末端描绘出的点的轨迹称为原始曲线的渐开线，而原始曲线称为其渐开线的渐屈线。上面以圆为例说明了这个过程。

虽然一条曲线只有一个唯一的渐屈线，但它有无数条渐开线，对应于初始点的不同选择。渐开线也可以被认为是与给定曲线的所有切线正交的任何曲线。

渐开线的方程是

(1)

其中 是切向量

(2)

和 是弧长

(3)

这可以写成参数表示函数 为

			(4)
			(5)

下表列出了一些常见曲线的渐开线，其中一些在上面进行了说明。