外摆线

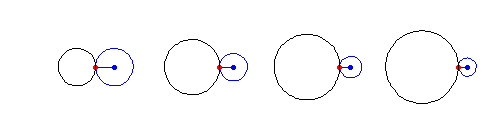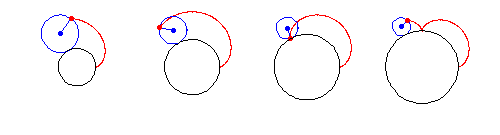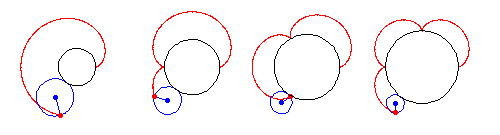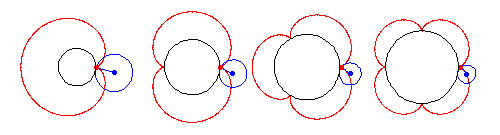
外摆线是由半径为 的圆上一点 在半径为 的圆外部滚动时所描绘的路径。因此，外摆线是 外旋轮线，其中 。外摆线由参数方程给出

			(1)
			(2)

可以通过计算导出极坐标方程

			(3)
			(4)

因此

(5)

但是

(6)

因此

			(7)
			(8)

请注意， 是这里的参数，不是极角。从中心开始的极角是

(9)

为了在外摆线中得到 个尖点，，因为这样 次 的旋转会将边缘上的点带回到其起始位置。

			(10)
			(11)
			(12)
			(13)

因此

			(14)
			(15)

具有一个尖点的外摆线称为心脏线，具有两个尖点的外摆线称为肾脏线，具有五个尖点的外摆线称为毛茛线。

外摆线也可以通过从圆的直径开始构造，并沿圆周以等弧长的一系列步长偏移一端，同时沿圆周以 倍大的步长偏移另一端。在围绕圆一周后，会产生 尖点外摆线的包络线，如上图所示（Madachy 1979）。

外摆线具有挠率

(16)

并满足

(17)

其中 是曲率半径 ()。